Neuronas

$\mathbf{\text{Definición.}}$ Sean $X,W\in {\mathbb{R}}^n$, $b\in \mathbb{R}$, $p:{\mathbb{R}}^n\to \mathbb{R}$ una función dada por: $$\begin{array}{}\text{(1)}& p(X)& =& \{\begin{array}{ll}0& \text{si }X\cdot W+b\le 0\\ 1& \text{si }X\cdot W+b>0\end{array}\end{array}$$ donde los elementos de $W$ se llaman pesos, $b$ se llama sesgo y $p$ se llama perceptrón.

$\mathbf{\text{Ejemplo.}}$ Sea $W=(-2,-2)$ y $b=3$, entonces

• $p((0,0))=1$
• $p((1,0))=1$
• $p((0,1))=1$
• $p((1,1))=0$

podemos observar que es equivalente a la función lógica NAND. Y como las puertas NAND son universales para el cálculo computacional, se deduce que los perceptrones también son universales para el cálculo computacional.

Observemos que del ejemplo previo, tenemos que es tranquilizador porque nos dice que las redes de perceptrones pueden ser tan potentes como cualquier otro dispositivo informático. Pero también es decepcionante, porque hace que parezca que los perceptrones son simplemente un nuevo tipo de puerta NAND. ¡Eso no es ninguna gran novedad! Sin embargo, la situación es mejor de lo que sugiere esta visión. Resulta que podemos diseñar algoritmos de aprendizaje que pueden ajustar automáticamente los pesos y sesgos de una red de neuronas artificiales.

$\mathbf{\text{Definición.}}$ Sean $X,W\in {\mathbb{R}}^n$, $b\in \mathbb{R}$, consideremos la función sigmoide $\sigma (z)=\frac{1}{1+e^{-z}}$, entonces una neurona sigmoide es $$\sigma (W\cdot X+b)=\frac{1}{1+e^{-W\cdot X-b}}$$

Observemos que: $$\underset{z\to \mathrm{\infty }}{lim}\sigma (z)=1\text{ y }\underset{z\to -\mathrm{\infty }}{lim}\sigma (z)=0$$

$\mathbf{\text{Definición.}}$ Sea $X\in {\mathbb{R}}^n$,$m\in \mathbb{N}$ y sea $L$ un conjunto de neuronas, $L=\{neuron{a}_1^l,\dots ,neuron{a}_m^l\}$ tal que $neuron{a}_i^l:{\mathbb{R}}^n\to \mathbb{R}$ para $i=1,\dots ,m$, entonces si evaluamos $X$ en cada neurona de $L$ se dice que $L$ es una capa.

Una red neuronal artificial totalmente conectada es la sucesión de una o más capas, digamos que la primera capa es $L$ y se conecta con la segunda capa $H$. Sean $L=\{neuron{a}_1^l,\dots ,neuron{a}_m^l\}$ y $H=\{neuron{a}_1^h,\dots ,neuron{a}_k^h\}$, entonces la salida de la primera capa es $$L(X)=\{neuron{a}_1^l(X),\dots ,neuron{a}_m^l(X)\}$$ y la salida de la segunda capa es $$H(L(X))=\{neuron{a}_1^h(L(X)),\dots ,neuron{a}_k^h(L(X)))\}$$ así sucesivamente para todas las capas de la red.

Aprendizaje

¿Cómo una red puede aprender a renocer digitos? con aprender nos referimos a que unos algoritmos ajusten automáticamente los pesos y sesgos de una red. Como ejemplo tomemos el conjunto de datos MNIST, el cual contiene 70,000 de miles de imagenes de digitos escritos a mano de 28 por 28 pixeles a escala de grises.

La entrada será $x$ un vector de 784 coordenadas (28$\times$28 = 784). Y la salida la denotaremos por $y(x)$, por ejemplo $y(x)=(0,1,0,0,0,0,0,0,0,0{)}^T$ corresponde a que el digito en $x$ es 2.

Lo que nos gustaría es un algoritmo que nos permita encontrar pesos y sesgos de modo que la salida de la red se aproxime a $y(x)$ epara todas las entradas de entrenamiento $x$. Para cuantificar qué tan bien estamos logrando este objetivo, definimos una $\mathbf{\text{función de costo}}$: $$\begin{array}{}\text{(1)}& C(w,b)\equiv \frac{1}{2n}\sum _x\Vert y(x)-a{\Vert }^2.\end{array}$$ Donde $y(x)$ es el valor esperado o el correcto correspondiente a $x$, las etiquetas que ya conocemos en el conjunto de entrenamiento y $a$ es la salida de la red dados los pesos y sesgos. La suma es sobre todas las entradas de entrenamiento. Llamaremos $C$ la función de costo cuadrático; a veces también se la conoce como error cuadrático medio o simplemente MSE.

Al examinar la forma de la función de costo cuadrático, vemos que $C(w,b)$ no es negativo, ya que cada término en la suma es no negativo. Además, el costo $C(w,b)$ se vuelve pequeño, es decir,$C(w,b)\approx 0$ , precisamente cuando $y(x)$ es aproximadamente igual al resultado, a , para todos los valores de entrada de entrenamiento, $x$ . Por lo tanto, nuestro algoritmo de entrenamiento ha hecho un buen trabajo si puede encontrar pesos y sesgos de modo que $C(w,b)\approx 0$ . Por el contrario, no lo está haciendo tan bien cuando $C(w,b)$ es grande, lo que significaría que $y(x)$ no está cerca del resultado a para una gran cantidad de valores de entrada. Por lo tanto, el objetivo de nuestro algoritmo de entrenamiento será minimizar el costo $C(w,b)$ como una función de los pesos y sesgos. En otras palabras, queremos encontrar un conjunto de pesos y sesgos que hagan que el costo sea lo más pequeño posible. Lo haremos utilizando un algoritmo conocido como descenso de gradiente.

Descenso del gradiente

Supongamos que $C:{\mathbb{R}}^2\to \mathbb{R}$ es una función derivable, sea $v\in {\mathbb{R}}^2$. Observemos que $$\begin{array}{}\text{(2)}& \mathrm{\Delta }C\approx \mathrm{\nabla }C\cdot \mathrm{\Delta }v.\end{array}$$ En lo que estamos interesados en escoger un $\mathrm{\Delta }v$ tal que haga $\mathrm{\Delta }C$ negativo, en particular supongamos que tomamos $$\begin{array}{}\text{(3)}& \mathrm{\Delta }v=-\eta \mathrm{\nabla }C,\end{array}$$ donde $\eta$ es un parámetro pequeño y positivo (conocido como $\mathbf{\text{tasa de aprendizaje}}$). Si sustituimos, entonces $$\mathrm{\Delta }C\approx -\eta \mathrm{\nabla }C\cdot \mathrm{\nabla }C=-\eta \Vert \mathrm{\nabla }C{\Vert }^2$$ como $\Vert \mathrm{\nabla }C{\Vert }^2\ge 0$, se garantiza que $\mathrm{\Delta }C\le 0$, es decir que $C$ siempre disminuye, si cambiamos $v$ según la prescripción en (3).

Entonces podemos actualizar $v$ de manera que disminuya $C$ de la siguiente manera $$v\to v^{\prime }=v-\eta \mathrm{\nabla }C$$ Si seguimos haciendo esto una y otra vez, seguiremos disminuyendo $C$ hasta que –esperemos– alcancemos un mínimo global.

¿Cómo podemos aplicar el descenso de gradiente para aprender en una red neuronal? La idea es utilizar el descenso de gradiente para encontrar los pesos $w_k$ y los sesgos $b_l$ que minimizan el costo en la ecuación (1). Para ver cómo funciona esto, reformulemos la regla de actualización del descenso de gradiente, con los pesos y los sesgos reemplazando las variables $v_j$ . En otras palabras, nuestra "posición" ahora tiene componentes $w_k$ y $b_l$ , y el vector de gradiente $\mathrm{\nabla }C$ tiene componentes correspondientes $\partial C/\partial w_k$ y $\partial C/\partial b_l$ . Escribiendo la regla de actualización del descenso de gradiente en términos de componentes, tenemos $$\begin{array}{rcl}{w}_k& \to & w_k^{\prime }=w_k-\eta \frac{\partial C}{\partial w_k}\\ b_l& \to & b_l^{\prime }=b_l-\eta \frac{\partial C}{\partial b_l}.\end{array}$$

Descenso de gradiente estocástico

Existen varios desafíos en la aplicación de la regla del descenso del gradiente. Los analizaremos en profundidad en capítulos posteriores. Pero por ahora solo quiero mencionar un problema. Para entender cuál es el problema, volvamos a analizar el costo cuadrático en la ecuación . Observe que esta función de costo tiene la forma $C=\frac{1}{n}\sum _x{C}_x$ , es decir, es un promedio de los costos $C_x=\frac{\Vert y(x)-a{\Vert }^2}{2}$ para ejemplos de entrenamiento individuales. En la práctica, para calcular el gradiente ∇C necesitamos calcular los gradientes $\mathrm{\nabla }{C}_x$ por separado para cada entrada de entrenamiento, $x$ , y luego promediarlos, $\mathrm{\nabla }C=\frac{1}{n}\sum _x\mathrm{\nabla }{C}_x$ . Desafortunadamente, cuando la cantidad de entradas de entrenamiento es muy grande, esto puede llevar mucho tiempo y, por lo tanto, el aprendizaje se produce lentamente.

Se puede utilizar una idea llamada descenso de gradiente estocástico para acelerar el aprendizaje. La idea es estimar el gradiente $\mathrm{\nabla }C$ calculando $\mathrm{\nabla }{C}_x$ para una pequeña muestra de entradas de entrenamiento elegidas al azar. Al promediar sobre esta pequeña muestra, resulta que podemos obtener rápidamente una buena estimación del gradiente real $\mathrm{\nabla }C$ , y esto ayuda a acelerar el descenso de gradiente y, por lo tanto, el aprendizaje.

Para que estas ideas sean más precisas, el descenso de gradiente estocástico funciona seleccionando aleatoriamente una pequeña cantidad $m$ de entradas de entrenamiento elegidas aleatoriamente. Etiquetaremos esas entradas de entrenamiento aleatorias $X_1,X_2,\dots ,X_m$ y las llamaremos minilote. Siempre que el tamaño de la muestra m sea lo suficientemente grande, esperamos que el valor promedio de $\mathrm{\nabla }C{X}_j$ sea aproximadamente igual al promedio de todos los $\mathrm{\nabla }Cx$ , es decir, $$\begin{array}{r}\frac{\sum _{j=1}^m\mathrm{\nabla }{C}_{X_j}}{m}\approx \frac{\sum _x\mathrm{\nabla }{C}_x}{n}=\mathrm{\nabla }C,\end{array}$$ donde la segunda suma corresponde a todo el conjunto de datos de entrenamiento. Entonces $$\begin{array}{r}\mathrm{\nabla }C\approx \frac{1}{m}\sum _{j=1}^m\mathrm{\nabla }{C}_{X_j},\end{array}$$ confirmando que podemos estimar el gradiente general calculando gradientes solo para el mini-lote elegido aleatoriamente.

Para conectar esto explícitamente con el aprendizaje en redes neuronales, supongamos que $w_k$ y $b_l$ denotan los pesos y sesgos en nuestra red neuronal. Entonces, el descenso de gradiente estocástico funciona seleccionando un minilote de entradas de entrenamiento elegidas al azar y entrenando con ellas. $$\begin{array}{rcl}{w}_k& \to & w_k^{\prime }=w_k-\frac{\eta }{m}\sum _j\frac{\partial C_{X_j}}{\partial w_k}\\ b_l& \to & b_l^{\prime }=b_l-\frac{\eta }{m}\sum _j\frac{\partial C_{X_j}}{\partial b_l},\end{array}$$

donde las sumas corresponden a todos los ejemplos de entrenamiento $X_j$ en el minibatch actual. Luego, elegimos otro minibatch elegido al azar y entrenamos con él. Y así sucesivamente, hasta que hayamos agotado las entradas de $\mathbf{\text{entrenamiento}}$, lo que se dice que completa una época de entrenamiento. En ese punto, comenzamos de nuevo con una nueva $\mathbf{\text{época de entrenamiento}}$.

Notación para la salida de una red

Comencemos con una notación que nos permite referirnos a los pesos de la red de una manera inequívoca. Usaremos $w_{jk}^l$ para indicar el peso de la conexión desde la neurona $k$-ésima en la capa $(l-1)$-ésima hasta la neurona $j$-ésima en la capa $l$-ésima.

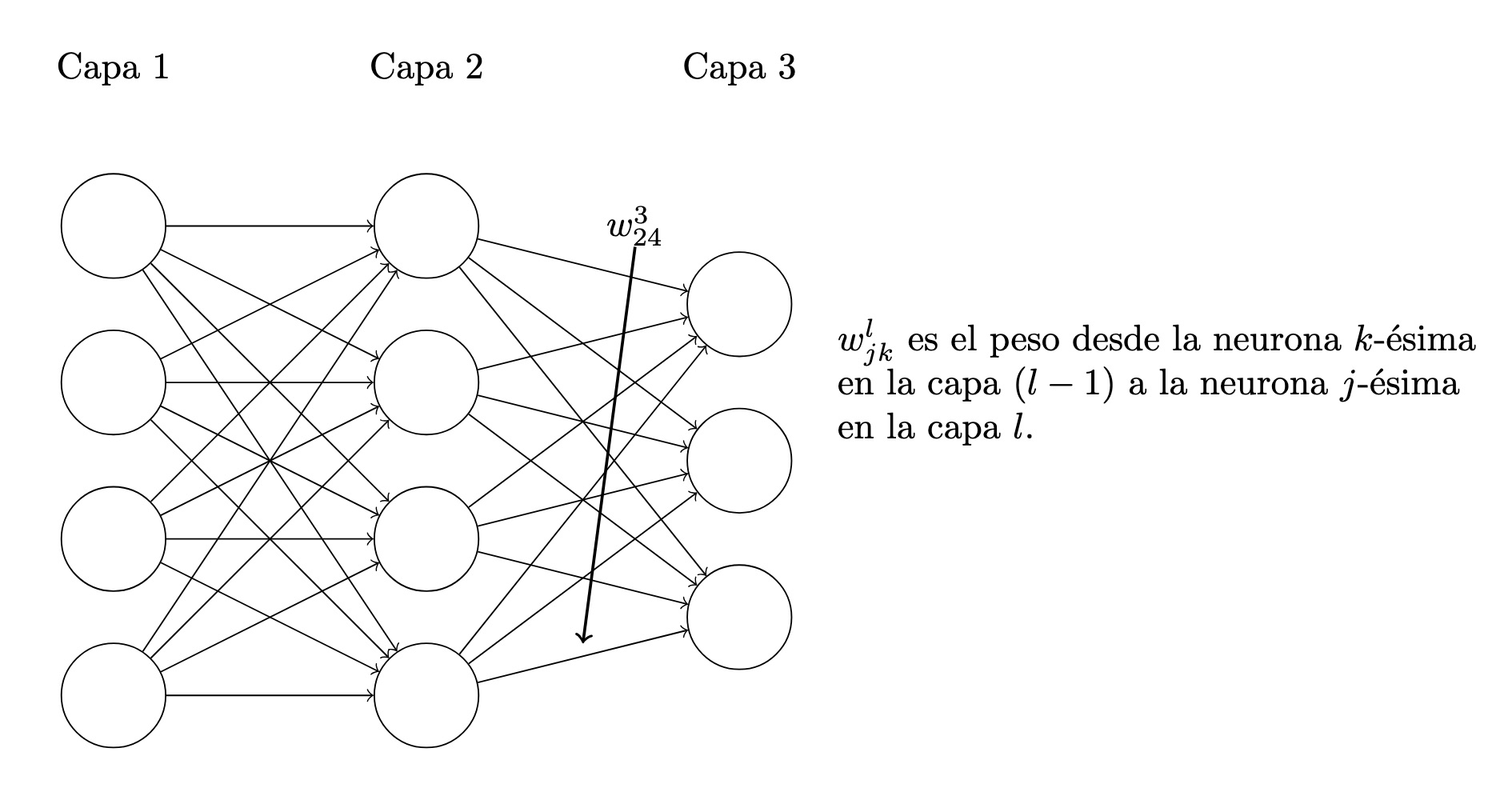
Utilizamos una notación similar para los sesgos y activaciones de la red. Explícitamente, utilizamos $b_j^l$ para el sesgo de la neurona $j$-ésima en la capa $l$-ésima. . Y utilizamos $a_j^l$ para la activación de la neurona $j$-ésima en la capa $l$-ésima.

Con estas notaciones, la activación $a_j^l$ de la neurona $j$-ésima en la capa $l$-ésima. está relacionada con las activaciones en la capa $(l-1)$-ésima mediante la ecuación $$\begin{array}{r}{a}_j^l=\sigma (\sum _k{w}_{jk}^l{a}_k^{l-1}+b_j^l),\end{array}$$

donde la suma es sobre todas las neuronas $k$ en la capa $(l-1)$-ésima . Para reescribir esta expresión en forma matricial definimos una matriz de pesos $w^l$ para cada capa, $l$ . Las entradas de la matriz de pesos $wl$ son solo los pesos que se conectan a la capa $l$-ésima de neuronas, es decir, la entrada en la fila $j$-ésima y la columna $k$-ésima es $w_{jk}^l$ . De manera similar, para cada capa $l$ definimos un vector de sesgos, $b^l$ . Probablemente puedas adivinar cómo funciona esto: los componentes del vector de polarización son solo los valores $b_j^l$ , un componente para cada neurona en la capa $l$-ésima . Y finalmente, definimos un vector de activación $a^l$ cuyos componentes son las activaciones $a_j^l$ .

Por otro lado, si $v$ es un vector, denotemos por $f(v)$ al vector resultante después de aplicar $f$ a cada componete de $v$, es decir $$\begin{array}{r}f\left(\left[\begin{array}{c}{v}_1\\ ⋮\\ v_n\end{array}\right]\right)=\left[\begin{array}{c}f(v_1)\\ ⋮\\ f(v_n)\end{array}\right]\end{array}$$

Entonces $$\begin{array}{r}{a}^l=\sigma (w^l{a}^{l-1}+b^l).\end{array}$$ Esta expresión nos da una forma mucho más global de pensar acerca de cómo las activaciones en una capa se relacionan con las activaciones en la capa anterior: simplemente aplicamos la matriz de pesos a las activaciones, luego agregamos el vector de sesgo y finalmente aplicamos la función $\sigma$.

Al utilizar la última ecuación para calcular $a^l$ , calculamos la cantidad intermedia $z^l=w^l{a}^{l-1}+b^l$ a lo largo del camino. Esta cantidad resulta ser lo suficientemente útil como para que valga la pena nombrarla: llamamos $z^l$ a la entrada ponderada a las neuronas en la capa $l$ .

El producto de Hadamard

Sea $x,y\in {\mathbb{R}}^n$, entonces la operación $\odot$ dada por $$x\odot y=(x_1{y}_1,\dots ,x_n{y}_n)$$ se llama producto de Hadamard o producto de Shur.

Suposiciones sobre la función de costo

Podemos reescribir la función de costo MSE con la nueva notación $$\begin{array}{r}C=\frac{1}{2n}\sum _x\Vert y(x)-a^L(x){\Vert }^2,\end{array}$$ La primera suposición que necesitamos es que la función de costo se puede escribir como un promedio $C=\frac{1}{n}\sum _x{C}_x$ sobre las funciones de costo $C_x$ para ejemplos de entrenamiento individuales,$x$ . Este es el caso de la función de costo cuadrática, donde el costo para un solo ejemplo de entrenamiento es $C_x=\frac{1}{2}\Vert y-a^L{\Vert }^2$.

La segunda suposición que hacemos sobre el costo es que puede escribirse como una función de las salidas de la red neuronal. Esta función de costo también depende de la salida deseada $y$ , y usted podría preguntarse por qué no consideramos el costo también como una función de $y$ . Sin embargo, recuerde que el ejemplo de entrenamiento de entrada $x$ es fijo, por lo que la salida $y$ también es un parámetro fijo. En particular, no es algo que podamos modificar cambiando los pesos y sesgos de ninguna manera, es decir, no es algo que la red neuronal aprenda. Por lo tanto, tiene sentido considerar $C$ como una función de las activaciones de salida $a^L$ únicamente, con $y$ simplemente un parámetro que ayuda a definir esa función.

Retropropagación

La retropropagación (o backpropagation) consiste en comprender cómo el cambio de pesos y sesgos en una red modifica la función de costo. En última instancia, esto significa calcular las derivadas parciales $\partial C/\partial w_{jk}^l$ y $\partial C/\partial b_j^l$ . Pero para calcularlas, primero introducimos una cantidad intermedia, ${\delta }_j^l$ , que llamamos error en la neurona $j$-ésima en la capa $l$-ésima . La retropropagación nos dará un procedimiento para calcular el error ${\delta }_j^l$ , y luego relacionará ${\delta }_j^l$ con $\partial C/\partial w_{jk}^l$ y $\partial C/\partial b_j^l$ .

Definimos el error ${\delta }_j^l$ de la neurona $j$ en la capa $l$ por $${\delta }_j^l\equiv \frac{\partial C}{\partial z_j^l}$$ Según nuestras convenciones habituales, utilizamos ${\delta }^l$ para denotar el vector de errores asociados con la capa $l$ .

$\mathbf{\text{Proposición.}}$ Dado lo anterior, tenemos como conscuencia las siguientes ecuaciones: $$\begin{array}{}\text{(1)}& {\delta }^L={\mathrm{\nabla }}_{a}C\odot {\sigma }^{\prime }(z^L)\end{array}$$ $$\begin{array}{}\text{(2)}& {\delta }^l=((w^{l+1}{)}^T{\delta }^{l+1})\odot {\sigma }^{\prime }(z^L)\end{array}$$ $$\begin{array}{}\text{(3)}& {\delta }_j^l=\frac{\partial C}{\partial b_j^l}\end{array}$$ $$\begin{array}{}\text{(4)}& \frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l.\end{array}$$

$\mathbf{\text{Demostración.}}$ 1) (Una ecuación para el error en la capa de salida). Supongamos que la capa de salida $L$ tiene $m$ neuronas, de la definición de ${\delta }_j^L$ y aplicando la regla de la cadena, podemos reexpresar la derivada parcial en términos de derivadas parciales con respecto a las activaciones de salida. Notemos que $$a_j^L=\sigma (z_j^L)\text{ y }C(a^L)=C(\sigma (z^L))$$ luego $$\begin{array}{rcl}{\delta }_j^L& =& \frac{\partial C}{\partial z_j^L}\\ & =& [\frac{\partial C}{\partial a_1^L},\dots ,\frac{\partial C}{\partial a_m^L}]{[\frac{\partial a_1^L}{\partial z_j^L},\dots ,\frac{\partial a_m^L}{\partial z_j^L}]}^T\\ & =& \sum _k\frac{\partial C}{\partial a_k^L}\frac{\partial a_k^L}{\partial z_j^L},\end{array}$$ donde la suma es sobre todas las neuronas $k$ en la capa de salida $L$. Por supuesto, la activación de salida $a_k^L$ de la neurona $k$-ésima depende solo de la entrada ponderada $z_j^L$ para la neurona $j$-ésima cuando $k=j$ . Y entonces $\partial a_k^L/\partial z_j^L$ se anula cuando $k\ne j$ . Como resultado, podemos simplificar la ecuación anterior a $${\delta }_j^L=\frac{\partial C}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}{\sigma }^{\prime }(z_j^L),$$ por lo tanto, $$\begin{array}{rcl}{\delta }^L& =& ({\delta }_1^L,\dots ,{\delta }_m^L)\\ & =& (\frac{\partial C}{\partial a_1^L},\dots ,\frac{\partial C}{\partial a_m^L})\odot ({\sigma }^{\prime }(z_1^L),\dots ,{\sigma }^{\prime }(z_m^L))\\ & =& {\mathrm{\nabla }}_{a}C\odot {\sigma }^{\prime }(z^L).\end{array}$$

2) que da una ecuación para el error ${\delta }^l$ en términos del error en la siguiente capa, ${\delta }^{l+1}$ . Para ello, queremos reescribir ${\delta }_j^l=\partial C/\partial z_j^l$ en términos de ${\delta }_k^{l+1}=\partial C/\partial z_k^{l+1}$ . Podemos hacer esto usando la regla de la cadena, $$\begin{array}{rcl}{\delta }_j^l& =& \frac{\partial C}{\partial z_j^l}\\ & =& \sum _k\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}\\ & =& \sum _k\frac{\partial z_k^{l+1}}{\partial z_j^l}{\delta }_k^{l+1},\end{array}$$ donde en la última línea hemos intercambiado los dos términos del lado derecho y hemos sustituido la definición de ${\delta }_k^{l+1}$ . Para evaluar el primer término en la última línea, tenga en cuenta que $$\begin{array}{rcl}{z}_k^{l+1}& =& \sum _j{w}_{kj}^{l+1}{a}_j^l+b_k^{l+1}\\ & =& \sum _j{w}_{kj}^{l+1}\sigma (z_j^l)+b_k^{l+1}.\end{array}$$ Diferenciando, obtenemos $$\begin{array}{r}\frac{\partial z_k^{l+1}}{\partial z_j^l}=w_{kj}^{l+1}{\sigma }^{\prime }(z_j^l).\end{array}$$ entonces $$\begin{array}{r}{\delta }_j^l=\sum _k{w}_{kj}^{l+1}{\delta }_k^{l+1}{\sigma }^{\prime }(z_j^l).\end{array}$$

3) (Una ecuación para la tasa de cambio del costo con respecto a cualquier sesgo en la red.) $$\begin{array}{rcl}\frac{\partial C}{\partial b_j^l}& =& \frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial b_j^l}\\ & =& \frac{\partial C}{\partial z_j^l}\frac{\partial (\sum _k{w}_{jk}^l\sigma (z_k^{l-1})+b_j^l)}{\partial b_j^l}\\ & =& \frac{\partial C}{\partial z_j^l}(\sum _k\frac{\partial (w_{jk}^l\sigma (z_k^{l-1}))}{\partial b_j^l}+\frac{\partial b_j^l}{\partial b_j^l})\\ & =& \frac{\partial C}{\partial z_j^l}(\sum _{k}0+1)=\frac{\partial C}{\partial z_j^l}={\delta }_j^l\end{array}$$

4) (Una ecuación para la tasa de cambio del costo con respecto a cualquier peso en la red.) $$\begin{array}{rcl}\frac{\partial C}{\partial w_{jk}^l}& =& \frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial w_{jk}^l}\\ & =& \frac{\partial C}{\partial z_j^l}\frac{\partial (\sum _m{w}_{jm}^l{a}_m^{l-1}+b_j^l)}{\partial w_{jk}^l}\\ & =& {\delta }_j^l[\left(\sum _m\frac{\partial (w_{jm}^l{a}_m^{l-1})}{\partial w_{jk}^l}\right)+\frac{\partial b_j^l}{\partial w_{jk}^l}]\\ & =& {\delta }_j^l[a_k^{l-1}\frac{\partial w_{jk}^l}{\partial w_{jk}^l}+0]\\ & =& {\delta }_j^l{a}_k^{l-1}.◻\end{array}$$

Observaciones

Hay otras ideas en esta línea que se pueden obtener de estas ecuaciones. Empecemos por observar la capa de salida. Consideremos el término ${\sigma }^{\prime }(z_j^L)$ en 1). Recordemos del gráfico de la función sigmoidea en el capítulo anterior que la función $\sigma$ se vuelve muy plana cuando $\sigma (z_j^L)$ es aproximadamente 0 o 1 . Cuando esto ocurre tendremos ${\sigma }^{\prime }(z_j^L)\approx 0$ . Y entonces la lección es que un peso en la capa final aprenderá lentamente si la neurona de salida tiene una activación baja $(\approx 0)$ o una activación alta $(\approx 1)$. En este caso es común decir que la neurona de salida se ha saturado y, como resultado, el peso ha dejado de aprender (o está aprendiendo lentamente). Observaciones similares también son válidas para los sesgos de la neurona de salida.

Podemos obtener información similar para capas anteriores. En particular, observe el término ${\sigma }^{\prime }(z^L)$ en 2). Esto significa que es probable que ${\delta }_j^l$ se vuelva pequeño si la neurona está cerca de la saturación. Y esto, a su vez, significa que cualquier peso ingresado a una neurona saturada aprenderá lentamente.

Resumiendo, hemos aprendido que un peso aprenderá lentamente si la neurona de entrada tiene baja activación o si la neurona de salida está saturada, es decir, tiene alta o baja activación.

Algoritmo de retropropagación

Las ecuaciones de retropropagación nos brindan una manera de calcular el gradiente de la función de costo. Escribámoslo explícitamente en forma de algoritmo:

• Entrada $x$: Establezca la activación correspondiente $a^1$ para la capa de entrada.
• Retroalimentación hacia adelante: Para cada $l=2,3,\dots ,L$ calcule $$z^l=w^l{a}^{l-1}+b^l\text{ y }{a}^l=\sigma (z^l).$$
• Error de salida ${\delta }^L$: calcule el vector $${\delta }^L={\mathrm{\nabla }}_{a}C\odot {\sigma }^{\prime }(z^L)$$
• Retropropagar el error:Para cada $l=L-1,L-2,\dots ,2$ calcular $${\delta }^l=((w^{l+1}{)}^T{\delta }^{l+1})\odot {\sigma }^{\prime }(z^l).$$
• Salida: El gradiente de la función de costo está dado por $$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l\text{ y }\frac{\partial C}{\partial b_j^l}={\delta }_j^l.$$

Al examinar el algoritmo, se puede ver por qué se llama retropropagación. Calculamos los vectores de error ${\delta }^l$ hacia atrás, comenzando desde la capa final. Puede parecer extraño que estemos recorriendo la red hacia atrás. Pero si piensa en la prueba de retropropagación, el movimiento hacia atrás es una consecuencia del hecho de que el costo es una función de las salidas de la red. Para entender cómo varía el costo con pesos y sesgos anteriores, necesitamos aplicar repetidamente la regla de la cadena, trabajando hacia atrás a través de las capas para obtener expresiones utilizables.

Retroprogación y descenso del grandiente estocástico

Como lo describí anteriormente, el algoritmo de retropropagación calcula el gradiente de la función de costo para un solo ejemplo de entrenamiento, $C=C_x$. En la práctica, es común combinar la retropropagación con un algoritmo de aprendizaje como el descenso de gradiente estocástico, en el que calculamos el gradiente para muchos ejemplos de entrenamiento. En particular, dado un minilote de $m$ ejemplos de entrenamiento, el siguiente algoritmo aplica un paso de aprendizaje de descenso de gradiente basado en ese minilote:

• Ingresar un conjunto de ejemplos de entrenamiento
• Para cada ejemplo de entrenamiento $x$ : Establezca la activación de entrada correspondiente $a^{x,1}$ , y realice los siguientes pasos:
• Feedforward: Para cada $l=2,3,\dots ,L$ calcule $$z^{x,l}=w^l{a}^{x,l-1}+b^l\text{ y }{a}^{x,l}=\sigma (z^{x,l}).$$
• Error de salida ${\delta }^{x,L}$ : Calcule el vector $${\delta }^{x,L}={\mathrm{\nabla }}_a{C}_x\odot {\sigma }^{\prime }(z^{x,L}).$$
• Retropropague el error: Para cada $l=L-1,L-2,\dots ,2$ calcule $${\delta }^{x,l}=((w^{l+1}{)}^T{\delta }^{x,l+1})\odot {\sigma }^{\prime }(z^{x,l}).$$
Descenso de gradiente: para cada $l=L,L-1,\dots ,2$ actualice los pesos según la regla $$w^l\to w^l-\frac{\eta }{m}\sum _x{\delta }^{x,l}(a^{x,l-1}{)}^T$$ , y los sesgos según la regla $$b^l\to b^l-\frac{\eta }{m}\sum _x{\delta }^{x,l}.$$

Estas son las ideas básicas de como funciona un red neuronal artificial de tipo feedforward (o Retroalimentación hacia adelante) para la tarea de clasificación. Pero existen otros problemas que surgen al implementar un modelo de este tipo, tales como:

• Elegir la función de costo.
• Métodos de regularización: esto para hacer que la red generalice mejor.
• Métodos para inicializar los pesos.
• ¿Cómo elegir los hiperparametros?: El número de capas y neuronas por cada capa, las funciones de activación, la tasa de aprendizaje, el número de epocas, etc.

La función de costo de entropía cruzada

Resulta que la función de costo MSE causa que la res aprenda muy lento, ya que observemos para el caso de tener solo una neurona $$\begin{array}{rcl}C(w,b)& =& \frac{1}{2n}\sum _x\Vert y(x)-a{\Vert }^2\\ & =& \frac{(y-a{)}^2}{2},\end{array}$$ Para escribir esto más explícitamente en términos de peso y sesgo, recuerde que $a=\sigma (z)$ , donde $z=wx+b$ . Usando la regla de la cadena para diferenciar con respecto al peso y el sesgo obtenemos $$\begin{array}{r}\frac{\partial C}{\partial w}=(a-y){\sigma }^{\prime }(z)x=a{\sigma }^{\prime }(z)\\ \frac{\partial C}{\partial b}=(a-y){\sigma }^{\prime }(z)x=a{\sigma }^{\prime }(z)\end{array}$$ donde se sustituyo $x=1$ y $y=0$. Para entender el conportamiento de estas expresiones, fijemonos en ${\sigma }^{\prime }(z)$, recordemos la forma de la función sigmoide: 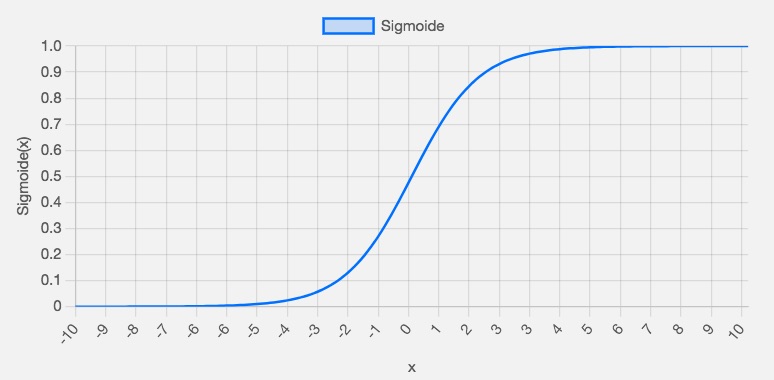En este gráfico podemos ver que cuando la salida de la neurona está cerca de 1 , la curva se vuelve muy plana y, por lo tanto, ${\sigma }^{\prime }(z)$ se vuelve muy pequeña. Las ecuaciones anteriores nos indican que las derivadas parciales se vuelven muy pequeñas. Este es el origen de la desaceleración del aprendizaje.

Definimos la función de costo de entropía cruzada por $$C=-\frac{1}{n}\sum _x[y\ln (a)+(1-y)\ln (1-a)]$$ donde $n$ es el número total de elementos de datos de entrenamiento, la suma es sobre todas las entradas de entrenamiento, $x$ , e $y$ es el resultado deseado correspondiente.

Dos propiedades en particular hacen que sea razonable interpretar la entropía cruzada como una función de costo. Primero, no es negativa, es decir, $C>0$. Para ver esto, observe que: (a) todos los términos individuales en la suma son negativos, ya que ambos logaritmos son de números en el rango de 0 a 1 ; y (b) hay un signo menos al principio de la suma.

En segundo lugar, si la salida real de la neurona es cercana a la salida deseada para todas las entradas de entrenamiento, $x$ , entonces la entropía cruzada será cercana a cero. Para ver esto, supongamos, por ejemplo, que $y=0$ y $a\approx 0$ para alguna entrada $x$ . Este es un caso en el que la neurona está haciendo un buen trabajo en esa entrada. Vemos que el primer término en la última expresión para el costo se desvanece, ya que $y=0$ , mientras que el segundo término es simplemente $-\ln (1-a)\approx 0$ . Un análisis similar se cumple cuando $y=1$ y $a\approx 1$ . Y entonces la contribución al costo será baja siempre que la salida real sea cercana a la salida deseada.

En resumen, la entropía cruzada es positiva y tiende a cero a medida que la neurona mejora en el cálculo de la salida deseada, $y$ , para todas las entradas de entrenamiento, $x$ . Ambas son propiedades que esperaríamos intuitivamente para una función de costo. De hecho, ambas propiedades también se satisfacen con el costo cuadrático. Por lo tanto, son buenas noticias para la entropía cruzada. Pero la función de costo de entropía cruzada tiene el beneficio de que, a diferencia del costo cuadrático, evita el problema de la desaceleración del aprendizaje. Para ver esto, calculemos la derivada parcial del costo de entropía cruzada con respecto a los pesos. Sustituimos $a=\sigma (z)$ $$\begin{array}{rcl}\frac{\partial C}{\partial w_j}& =& -\frac{1}{n}\sum _x(\frac{y}{\sigma (z)}-\frac{(1-y)}{1-\sigma (z)})\frac{\partial \sigma }{\partial w_j}\\ & =& -\frac{1}{n}\sum _x(\frac{y}{\sigma (z)}-\frac{(1-y)}{1-\sigma (z)}){\sigma }^{\prime }(z)x_j.\end{array}$$ entonces $$\begin{array}{rcl}\frac{\partial C}{\partial w_j}& =& \frac{1}{n}\sum _x\frac{{\sigma }^{\prime }(z)x_j}{\sigma (z)(1-\sigma (z))}(\sigma (z)-y).\end{array}$$

Proposición. ${\sigma }^{\prime }(z)=\sigma (z)(1-\sigma (z))$

Demostración. Tenemos que $\sigma (z)={\displaystyle \frac{1}{1+e^{-z}}}$, entonces $$\begin{array}{rcl}{\sigma }^{\prime }(z)& =& \frac{0(1+e^{-z})-(-e^{-z})}{(1+e^{-z}{)}^2}\\ & =& \frac{e^{-z}}{(1+e^{-z})(1+e^{-z})}\\ & =& \frac{1}{1+e^{-z}}\left(\frac{e^{-z}}{1+e^{-z}}\right)\\ & =& \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})\\ & =& \sigma (z)(1-\sigma (z)).\end{array}$$

Entonces $$\begin{array}{r}\frac{\partial C}{\partial w_j}=\frac{1}{n}\sum _x{x}_j(\sigma (z)-y).\end{array}$$ Esta es una expresión hermosa. Nos dice que la velocidad a la que aprende el peso está controlada por $\sigma (z)-y$ , es decir, por el error en la salida. Cuanto mayor sea el error, más rápido aprenderá la neurona. Esto es justo lo que esperaríamos intuitivamente. En particular, evita la desaceleración del aprendizaje causada por el término ${\sigma }^{\prime }(z)$ en la ecuación análoga para el costo cuadrático. Cuando usamos la entropía cruzada, el término ${\sigma }^{\prime }(z)$ se cancela y ya no tenemos que preocuparnos por si es pequeño. Esta cancelación es el milagro especial garantizado por la función de costo de entropía cruzada. En realidad, no es realmente un milagro. Como veremos más adelante, la entropía cruzada fue elegida especialmente para tener precisamente esta propiedad.

De manera similar, podemos calcular la derivada parcial del sesgo. No entraré en detalles nuevamente, pero puedes comprobarlo fácilmente. $$\begin{array}{r}\frac{\partial C}{\partial b}=\frac{1}{n}\sum _x(\sigma (z)-y).\end{array}$$

Hemos estado estudiando la entropía cruzada para una sola neurona. Sin embargo, es fácil generalizar la entropía cruzada a redes multicapa de muchas neuronas. En particular, supongamos que $y=y_1,y_2,\dots$ son los valores deseados en las neuronas de salida, es decir, las neuronas en la capa final, mientras que $a^{L_1},a^{L_2},\dots$ son los valores de salida reales. Luego definimos la entropía cruzada mediante $$\begin{array}{r}C=-\frac{1}{n}\sum _x\sum _j[y_j\ln a_j^L+(1-y_j)\ln (1-a_j^L)].\end{array}$$ Y calculando la derivada respecto a los pesos tenemos $$\begin{array}{}\text{(5)}& \frac{\partial C}{\partial w_{jk}^L}& =& \frac{1}{n}\sum _x{a}_k^{L-1}(a_j^L-y_j).\end{array}$$

¿Qué pasa con el significado intuitivo de la entropía cruzada? ¿Cómo deberíamos pensar en ello? Explicarlo en profundidad nos llevaría más lejos de lo que quiero llegar. Sin embargo, vale la pena mencionar que existe una forma estándar de interpretar la entropía cruzada que proviene del campo de la teoría de la información. En términos generales, la idea es que la entropía cruzada es una medida de sorpresa.

Softmax

Otro enfoque del problema de aprendizaje lento es basado en lo que se denomina capas softmax de neuronas. No aplicamos la función sigmoidea para obtener la salida. En cambio, en una capa softmax aplicamos la llamada función softmax a $z_j^L$ . Según esta función, la activación $a_j^L$ de la neurona de salida $j$-ésima es $$\begin{array}{r}{a}_j^L=\frac{e^{z_j^L}}{\sum _k{e}^{z_k^L}},\end{array}$$ donde en el denominador sumamos todas las neuronas de salida.

Observemos que $$\begin{array}{r}\sum _j{a}_j^L=\frac{\sum _j{e}^{z_j^L}}{\sum _k{e}^{z_k^L}}=1\end{array}$$ Como resultado, si $a_j^L$ aumenta, entonces las otras activaciones de salida deben disminuir en la misma cantidad total, para asegurar que la suma de todas las activaciones permanezca en 1 . Y, por supuesto, afirmaciones similares se aplican a todas las demás activaciones. La ecuación también implica que las activaciones de salida son todas positivas, ya que la función exponencial es positiva. Combinando esto, vemos que la salida de la capa softmax es un conjunto de números positivos que suman 1 . En otras palabras, la salida de la capa softmax puede considerarse como una distribución de probabilidad.

Para entender como esto ayuda para el problema de aprendizaje lento, definamos la función de costo de verosimilitud logarítmica. Usaremos $x$ para indicar una entrada de entrenamiento para la red, e $y$ para indicar la salida deseada correspondiente. Entonces, el costo de verosimilitud logarítmica asociado a esta entrada de entrenamiento es $$\begin{array}{r}C\equiv -\ln a_y^L.\end{array}$$

Por ejemplo, si estamos entrenando con imágenes MNIST y le metemos una imagen de un 7 , entonces el costo de verosimilitud logarítmica es $-\ln (a_7^L)$ . Para ver que esto tiene sentido intuitivo, considere el caso en el que la red está haciendo un buen trabajo, es decir, está segura de que la entrada es un 7 . En ese caso, estimará un valor para la probabilidad correspondiente $a_7^L$ que es cercano a 1 , por lo que el costo $-\ln (a_7^L)$ será pequeño. Por el contrario, cuando la red no está haciendo un buen trabajo, la probabilidad $a_7^L$ será menor y el costo $-\ln (a_7^L)$ será mayor. Por lo tanto, el costo de verosimilitud logarítmica se comporta como esperaríamos que se comportara una función de costo.

Podemos mostrar que $$\begin{array}{rcl}\frac{\partial C}{\partial b_j^L}& =& a_j^L-y_j\\ \frac{\partial C}{\partial w_{jk}^L}& =& a_k^{L-1}(a_j^L-y_j)\end{array}$$ Si comparamos la última ecuación con la ecuación (5), vemos que es la misma ecuación, aunque en la última he promediado las instancias de entrenamiento. Y, al igual que en el análisis anterior, estas expresiones garantizan que no nos encontraremos con una desaceleración del aprendizaje. De hecho, es útil pensar en una capa de salida softmax con un costo de verosimilitud logarítmica como algo bastante similar a una capa de salida sigmoidea con un costo de entropía cruzada.

Sobreajuste

La cuestión, por supuesto, es que los modelos con una gran cantidad de parámetros libres pueden describir una gama sorprendentemente amplia de fenómenos. Incluso si un modelo de este tipo concuerda bien con los datos disponibles, eso no lo convierte en un buen modelo. Puede significar simplemente que hay suficiente libertad en el modelo como para que pueda describir casi cualquier conjunto de datos del tamaño dado, sin capturar ninguna perspectiva genuina sobre el fenómeno subyacente. Cuando eso sucede, el modelo funcionará bien con los datos existentes, pero no podrá generalizarse a nuevas situaciones. La verdadera prueba de un modelo es su capacidad para hacer predicciones en situaciones a las que no ha estado expuesto antes.

En el caso de un red para clasificar podemos observar el accuracy en conjunto de test a lo largo de las epocas y ver cuando deja de mejorar. Entonces si la red no mejora después de la $n$-ésima época, se dice que la red no generaliza más en el conjunto de test. Decimos que la red está sobreajustada (overfitting) o sobreentrenada después de la época $n$.

También podemos observar la función de costo a largo de las épocas sobre el conjunto de entrenamiento y de test. Mientras que el primer conjunto sigue mejorando, en el segundo en cierta época alcanza un mínimo y luego empeora.

Otra manera es ver el accuracy en el conjunto de entrenamiento y de test. Mientras que en el primero puede tener 100% en el segundo puede tener 80% o menos. De modo que nuestra red realmente está aprendiendo acerca de las peculiaridades del conjunto de entrenamiento, no solo reconociendo dígitos en general. Es casi como si nuestra red simplemente estuviera memorizando el conjunto de entrenamiento, sin comprender los dígitos lo suficientemente bien como para generalizarlos al conjunto de prueba.

La forma obvia de detectar el sobreajuste es utilizar el enfoque anterior, haciendo un seguimiento de la precisión de los datos de prueba a medida que nuestra red se entrena. Si vemos que la precisión de los datos de prueba ya no mejora, entonces debemos detener el entrenamiento. Por supuesto, estrictamente hablando, esto no es necesariamente una señal de sobreajuste. Puede ser que la precisión de los datos de prueba y de los datos de entrenamiento dejen de mejorar al mismo tiempo. Aun así, adoptar esta estrategia evitará el sobreajuste.

Hasta ahora hemos estado usando training_data y test_data, e ignorando validation_data. validation_data contiene 10 000 imágenes de dígitos, imágenes que son diferentes de las 50 000 imágenes en el conjunto de entrenamiento MNIST y las 10 000 imágenes en el conjunto de prueba MNIST. En lugar de usar test_data para evitar el sobreajuste, usaremos el conjunto de validación, validation_data. Para ello, usaremos la misma estrategia que se describió anteriormente para test_data. Es decir, calcularemos la precisión de clasificación en validation_data al final de cada época. Una vez que la precisión de clasificación en validation_data se ha saturado, detenemos el entrenamiento. Esta estrategia se llama detención temprana. Por supuesto, en la práctica no sabremos inmediatamente cuándo se ha saturado la precisión. En cambio, continuamos con el entrenamiento hasta que estemos seguros de que la precisión se ha saturado.

¿Por qué utilizar los datos de validación para evitar el sobreajuste, en lugar de los datos de prueba? De hecho, esto forma parte de una estrategia más general, que consiste en utilizar los datos de validación para evaluar diferentes opciones de prueba de hiperparámetros, como la cantidad de épocas para las que se realizará el entrenamiento, la tasa de aprendizaje, la mejor arquitectura de red, etc.

Por supuesto, eso no responde de ninguna manera a la pregunta de por qué estamos usando validation_data para evitar el sobreajuste, en lugar de test_data. En cambio, la reemplaza con una pregunta más general, que es por qué estamos usando validation_data en lugar de test_data para establecer buenos hiperparámetros. Para entender por qué, considere que al establecer hiperparámetros es probable que probemos muchas opciones diferentes para los hiperparámetros. Si establecemos los hiperparámetros en función de las evaluaciones de test_data, es posible que terminemos sobreajustando nuestros hiperparámetros a test_data. Es decir, podemos terminar encontrando hiperparámetros que se ajusten a peculiaridades particulares de test_data, pero donde el rendimiento de la red no se generalice a otros conjuntos de datos. Nos protegemos contra eso al determinar los hiperparámetros utilizando validation_data. Luego, una vez que tenemos los hiperparámetros que queremos, hacemos una evaluación final de precisión utilizando test_data. Eso nos da la confianza de que nuestros resultados en los datos de prueba son una verdadera medida de qué tan bien se generaliza nuestra red neuronal. Dicho de otro modo, puedes pensar en los datos de validación como un tipo de datos de entrenamiento que nos ayudan a aprender buenos hiperparámetros. Este enfoque para encontrar buenos hiperparámetros a veces se conoce como el método de retención o held out, ya que los datos de validación se mantienen separados o "retenidos" de los datos de entrenamiento.

Regularización

Aumentar la cantidad de datos de entrenamiento es una forma de reducir el sobreajuste. ¿Existen otras formas de reducir el grado en que se produce el sobreajuste? Un enfoque posible es reducir el tamaño de nuestra red. Sin embargo, las redes grandes tienen el potencial de ser más potentes que las redes pequeñas, por lo que esta es una opción que solo adoptaríamos con reticencia. Afortunadamente, existen otras técnicas que pueden reducir el sobreajuste, incluso cuando tenemos una red fija y datos de entrenamiento fijos. Estas se conocen como técnicas de regularización.

L2

Una técnica que a veces se conoce como decaimiento de peso o regularización L2. La idea de la regularización L2 es agregar un término adicional a la función de costo, un término llamado término de regularización. Aquí está la entropía cruzada regularizada: $$\begin{array}{r}C=-\frac{1}{n}\sum _{x_j}[y_j\ln a_j^L+(1-y_j)\ln (1-a_j^L)]+\frac{\lambda }{2n}\sum _w{w}^2.\end{array}$$ El primer término es simplemente la expresión habitual de la entropía cruzada, pero hemos añadido un segundo término, es decir, la suma de los cuadrados de todos los pesos de la red. Esto se escala mediante un factor $\lambda /2n$ , donde $\lambda >0$ se conoce como el parámetro de regularización y $n$ es, como es habitual, el tamaño de nuestro conjunto de entrenamiento. Más adelante analizaré cómo se elige $\lambda$ . También vale la pena señalar que el término de regularización no incluye los sesgos.

Por supuesto, es posible regularizar otras funciones de costo, como el costo cuadrático. Esto se puede hacer de manera similar. $$\begin{array}{r}C=\frac{1}{2n}\sum _x\Vert y-a^L{\Vert }^2+\frac{\lambda }{2n}\sum _w{w}^2.\end{array}$$ En ambos casos podemos escribir la función de costo regularizada como $$\begin{array}{r}C=C_0+\frac{\lambda }{2n}\sum _w{w}^2,\end{array}$$ donde $C_0$ es la función de costo original no regularizada.

Intuitivamente, el efecto de la regularización es hacer que la red prefiera aprender pesos pequeños, en igualdad de condiciones. Los pesos grandes solo se permitirán si mejoran considerablemente la primera parte de la función de costo. Dicho de otra manera, la regularización puede verse como una forma de compromiso entre encontrar pesos pequeños y minimizar la función de costo original. La importancia relativa de los dos elementos del compromiso depende del valor de $\lambda$ : cuando $\lambda$ es pequeño, preferimos minimizar la función de costo original, pero cuando $\lambda$ es grande, preferimos pesos pequeños.

Para construir un ejemplo de este tipo, primero debemos averiguar cómo aplicar nuestro algoritmo de aprendizaje de descenso de gradiente estocástico en una red neuronal regularizada. En particular, necesitamos saber cómo calcular las derivadas parciales. $$\begin{array}{rcl}\frac{\partial C}{\partial w}& =& \frac{\partial C_0}{\partial w}+\frac{\lambda }{n}w\\ \frac{\partial C}{\partial b}& =& \frac{\partial C_0}{\partial b}.\end{array}$$ Y así la regla de aprendizaje del descenso del gradiente es: $$\begin{array}{rcl}b& \to & b-\eta \frac{\partial C_0}{\partial b}.\end{array}$$ $$\begin{array}{rcl}w& \to & w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda }{n}w\\ & =& (1-\frac{\eta \lambda }{n})w-\eta \frac{\partial C_0}{\partial w}.\end{array}$$ Esto es exactamente lo mismo que la regla de aprendizaje de descenso de gradiente habitual, excepto que primero reescalamos el peso $w$ por un factor $1-\frac{\eta \lambda }{n}$ . Este reescalamiento a veces se denomina decaimiento de peso, ya que hace que los pesos sean más pequeños.

Por lo tanto, la regla de aprendizaje regularizada para el descenso de gradiente estocástico se convierte en $$\begin{array}{r}w\to (1-\frac{\eta \lambda }{n})w-\frac{\eta }{m}\sum _x\frac{\partial C_x}{\partial w},\end{array}$$ donde la suma es sobre los ejemplos de entrenamiento $x$ en el mini-lote, y $C_x$ es el costo (no regularizado) para cada ejemplo de entrenamiento.Por último, y para completar, permítanme enunciar la regla de aprendizaje regularizada para los sesgos. Ésta es, por supuesto, exactamente la misma que en el caso no regularizado. $$\begin{array}{r}b\to b-\frac{\eta }{m}\sum _x\frac{\partial C_x}{\partial b},\end{array}$$ donde la suma es sobre los ejemplos de entrenamiento $x$ en el mini-lote.

¿Por qué ocurre esto? Heurísticamente, si la función de costo no está regularizada, entonces es probable que la longitud del vector de peso crezca, si todo lo demás permanece igual. Con el tiempo, esto puede hacer que el vector de peso sea realmente muy grande. Esto puede hacer que el vector de peso se quede atascado apuntando más o menos en la misma dirección, ya que los cambios debidos al descenso del gradiente solo producen cambios minúsculos en la dirección, cuando la longitud es grande. Creo que este fenómeno dificulta que nuestro algoritmo de aprendizaje explore adecuadamente el espacio de pesos y, en consecuencia, que encuentre buenos mínimos de la función de costo.

¿Cómo L2 reduce el sobreajuste?

Antes comentemos que datos un conjunto de pocos puntos, digamos 9, podríamos calcular un polinomio de grado 9 que se ajuste perfectamente a los datos y supongamos que también una recta se aproxima bien a cada punto. ¿Cuál es el mejor modelo? depende del fénomeno que se pretende modelar. Ahora si hacemos una predicción para un valor mucho mayor fuera de los datos originales tendriamos una gran diferencia en estos dos modelos. Una forma de decirlo es que el polinomio es demasiado complejo que es malo para generalizar mientras que el otro es más simple.

Veamos qué significa este punto de vista para las redes neuronales. Supongamos que nuestra red tiene en su mayoría pesos pequeños, como tenderá a suceder en una red regularizada. La pequeñez de los pesos significa que el comportamiento de la red no cambiará demasiado si cambiamos algunas entradas aleatorias aquí y allá. Eso hace que sea difícil para una red regularizada aprender los efectos del ruido local en los datos. Piense en esto como una forma de hacer que las piezas individuales de evidencia no importen demasiado para el resultado de la red. En cambio, una red regularizada aprende a responder a tipos de evidencia que se ven a menudo en el conjunto de entrenamiento. Por el contrario, una red con pesos grandes puede cambiar su comportamiento bastante en respuesta a pequeños cambios en la entrada. Y así, una red no regularizada puede usar pesos grandes para aprender un modelo complejo que lleva mucha información sobre el ruido en los datos de entrenamiento. En pocas palabras, las redes regularizadas están limitadas a construir modelos relativamente simples basados en patrones que se ven a menudo en los datos de entrenamiento y son resistentes al aprendizaje de las peculiaridades del ruido en los datos de entrenamiento. La esperanza es que esto obligue a nuestras redes a realizar un aprendizaje real sobre el fenómeno en cuestión y a generalizar mejor a partir de lo aprendido.

Dicho esto, esta idea de preferir explicaciones más simples debería ponerte nervioso. A veces la gente se refiere a esta idea como la "navaja de Occam" y la aplica con celo como si tuviera el estatus de un principio científico general. Pero, por supuesto, no es un principio científico general. No hay ninguna razón lógica a priori para preferir explicaciones simples a explicaciones más complejas. De hecho, a veces la explicación más compleja resulta ser la correcta.

Nadie ha desarrollado aún una explicación teórica totalmente convincente de por qué la regularización ayuda a las redes a generalizarse.

L1

Regularización L1: En este enfoque modificamos la función de costo no regularizada agregando la suma de los valores absolutos de los pesos: $$\begin{array}{r}C=C_0+\frac{\lambda }{n}\sum _w|w|.\end{array}$$ Diferenciando obtenemos $$\begin{array}{r}\frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda }{n}\mathrm{s}\mathrm{g}\mathrm{n}(w),\end{array}$$ donde $sgn(w)$ es el signo de $w$, es decir, +1 si $w$ es positivo y −1 si $w$ es negativo. Con esta expresión, podemos modificar fácilmente la retropropagación para realizar un descenso de gradiente estocástico utilizando la regularización L1. La regla de actualización resultante es $$\begin{array}{r}w\to w^{\prime }=w-\frac{\eta \lambda }{n}\text{sgn}(w)-\eta \frac{\partial C_0}{\partial w},\end{array}$$ En la regularización L1, los pesos se reducen en una cantidad constante hacia 0 . En la regularización L2, los pesos se reducen en una cantidad que es proporcional a $w$ . Y entonces, cuando un peso particular tiene una magnitud grande, $|w|$ , la regularización L1 reduce el peso mucho menos que la regularización L2. Por el contrario, cuando $|w|$ es pequeño, la regularización L1 reduce el peso mucho más que la regularización L2. El resultado neto es que la regularización L1 tiende a concentrar el peso de la red en una cantidad relativamente pequeña de conexiones de alta importancia, mientras que los otros pesos se dirigen hacia cero.

Dropout

En el dropout modificamos la propia red. En particular, supongamos que tenemos una entrada de entrenamiento $x$ y una salida deseada correspondiente $y$ . Normalmente, entrenaríamos propagando hacia adelante $x$ a través de la red y luego retropropagando para determinar la contribución al gradiente. Con la eliminación, este proceso se modifica. Comenzamos eliminando aleatoriamente (y temporalmente) la mitad de las neuronas ocultas en la red, mientras dejamos intactas las neuronas de entrada y salida. Después de hacer esto, terminaremos con una red similar a la siguiente. Tenga en cuenta que las neuronas que se eliminan temporalmente, siguen estando ocultas:

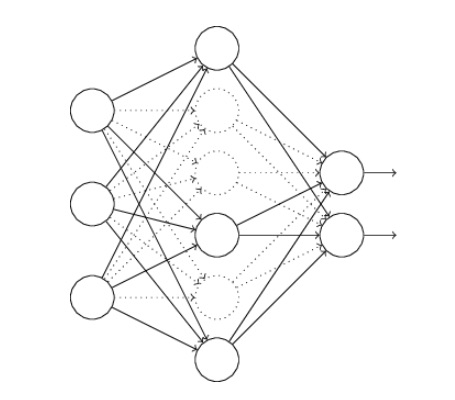
Propagamos hacia adelante la entrada $x$ a través de la red modificada y luego retropropagamos el resultado, también a través de la red modificada. Después de hacer esto en un minilote de ejemplos, actualizamos los pesos y sesgos apropiados. Luego repetimos el proceso, primero restaurando las neuronas abandonadas, luego eligiendo un nuevo subconjunto aleatorio de neuronas ocultas para eliminar, estimando el gradiente para un minilote diferente y actualizando los pesos y sesgos en la red.

Al repetir este proceso una y otra vez, nuestra red aprenderá un conjunto de pesos y sesgos. Por supuesto, esos pesos y sesgos se habrán aprendido en condiciones en las que se eliminaron la mitad de las neuronas ocultas. Cuando realmente ejecutamos la red completa, eso significa que el doble de neuronas ocultas estarán activas. Para compensar eso, reducimos a la mitad los pesos salientes de las neuronas ocultas.

Heurísticamente, cuando eliminamos diferentes conjuntos de neuronas, es como si estuviéramos entrenando diferentes redes neuronales. Por lo tanto, el procedimiento de deserción es como promediar los efectos de una gran cantidad de redes diferentes. Las diferentes redes se sobreajustarán de diferentes maneras y, por lo tanto, es de esperar que el efecto neto de la deserción sea reducir el sobreajuste.

Una explicación heurística relacionada con el abandono se da en uno de los primeros artículos que utilizan la técnica."Esta técnica reduce las complejas coadaptaciones de las neuronas, ya que una neurona no puede depender de la presencia de otras neuronas en particular. Por lo tanto, se ve obligada a aprender características más robustas que son útiles en conjunción con muchos subconjuntos aleatorios diferentes de las otras neuronas". En otras palabras, si pensamos en nuestra red como un modelo que está haciendo predicciones, entonces podemos pensar en la pérdida como una forma de asegurarnos de que el modelo sea robusto ante la pérdida de cualquier pieza individual de evidencia. En esto, es algo similar a la regularización L1 y L2, que tienden a reducir los pesos y, por lo tanto, hacen que la red sea más robusta ante la pérdida de cualquier conexión individual en la red.

Ampliación artificial de los datos de entrenamiento

Podemos ampliar nuestros datos de entrenamiento realizando muchas rotaciones pequeñas de todas las imágenes de entrenamiento MNIST y luego usar los datos de entrenamiento ampliados para mejorar el rendimiento de nuestra red.Pero también trasladar y distorsionar las imágenes.

Se pueden utilizar variaciones de esta idea para mejorar el rendimiento en muchas tareas de aprendizaje, no solo en el reconocimiento de escritura a mano. El principio general es ampliar los datos de entrenamiento aplicando operaciones que reflejen la variación del mundo real. No es difícil pensar en formas de hacerlo. Supongamos, por ejemplo, que estamos construyendo una red neuronal para realizar el reconocimiento de voz. Los humanos podemos reconocer el habla incluso en presencia de distorsiones, como el ruido de fondo. Por lo tanto, podemos ampliar nuestros datos añadiendo ruido de fondo. También podemos reconocer el habla si se acelera o se ralentiza. Así que esa es otra forma de ampliar los datos de entrenamiento.

Inicialización de pesos

Cuando creamos nuestras redes neuronales, tenemos que elegir los pesos y sesgos iniciales.Una prescripción consiste en elegir tanto los pesos como los sesgos utilizando variables aleatorias gaussianas independientes, normalizadas para tener una media de 0 y una desviación estándar de 1 . Si bien este enfoque funciona bien, vale la pena revisarlo para ver si podemos encontrar una mejor manera de establecer nuestros pesos y sesgos iniciales, y tal vez ayudar a nuestras redes neuronales a aprender más rápido.

Veamos un ejemplo, supongamos que la entrada de la red son 1000 neuronas de entrada y una $x$ tal que la mitad de estas neuronas resultan en 1 y la otra mitad en 0. Con los pesos inicializados con la distribución gaussiana como mencionamos arriba.

Tomemos la entrada de una neurona en la primera capa oculta $z=\sum _j{z}_j{w}_j+b$ donde $b=1$, entonces $z=501$. Por lo tanto, $z$ se distribuye como una gaussiana con media cero y desviación estándar $\sqrt{501}\approx 22.4$. Luego la $|z|$ es muy probable que sea grande, enotnces la salida de esta neurona $\sigma (z)$ estaría muy cerca de 0 o 1. Esto significa que la neurona esta saturada.

Y cuando eso sucede, como sabemos, hacer pequeños cambios en los pesos solo producirá cambios absolutamente minúsculos en la activación de nuestra neurona oculta. Ese cambio minúsculo en la activación de la neurona oculta, a su vez, apenas afectará al resto de las neuronas de la red, y veremos un cambio correspondientemente minúsculo en la función de costo. Como resultado, esos pesos solo aprenderán muy lentamente cuando usemos el algoritmo de descenso de gradiente.

Argumentos similares se aplican también a capas ocultas posteriores: si los pesos en capas ocultas posteriores se inicializan utilizando gaussianas normalizadas, entonces las activaciones a menudo serán muy cercanas a 0 o 1 , y el aprendizaje procederá muy lentamente.

Supongamos que tenemos una neurona con $n_{in}$ pesos de entrada . Luego, inicializaremos esos pesos como variables aleatorias gaussianas con media 0 y desviación estándar $1/\sqrt{n_{in}}$.Continuaremos eligiendo el sesgo como gaussiano con media 0 y desviación estándar 1. Supongamos, como hicimos antes, que 500 de las entradas son cero y 500 son 1 . Entonces es fácil demostrar que $z$ tiene una distribución gaussiana con media 0 y desviación estándar $\sqrt{3/2}=1.22\dots$. Esto tiene un pico mucho más pronunciado que antes. Es mucho menos probable que una neurona así se sature y, en consecuencia, mucho menos probable que tenga problemas con una ralentización del aprendizaje.

¿Cómo elegir los hiperparámetros de una red neuronal?

Es fácil sentirse perdido en el espacio de los hiperparámetros. Esto puede ser particularmente frustrante si su red es muy grande o utiliza muchos datos de entrenamiento, ya que puede entrenar durante horas, días o semanas y no obtener ningún resultado.

Por ejemplo, supongamos que estás atacando MNIST por primera vez. Comienzas entusiasmado, pero te desanimas un poco cuando tu primera red falla por completo, como en el ejemplo anterior. El camino a seguir es simplificar el problema. Deshazte de todas las imágenes de entrenamiento y validación, excepto las imágenes que son 0 o 1. Luego, intenta entrenar una red para que distinga los 0 de los 1. No solo es un problema inherentemente más fácil que distinguir los diez dígitos, sino que también reduce la cantidad de datos de entrenamiento en un 80 por ciento, acelerando el entrenamiento por un factor de 5. Eso permite una experimentación mucho más rápida y, por lo tanto, te da una idea más rápida de cómo construir una buena red.

Puedes conseguir otra aceleración en la experimentación aumentando la frecuencia de monitorización. Por supuesto, diez segundos no es mucho tiempo, pero si quieres probar docenas de opciones de hiperparámetros es molesto, y si quieres probar cientos o miles de opciones empieza a resultar agotador. Podemos obtener retroalimentación más rápidamente si monitoreamos la precisión de la validación con mayor frecuencia, por ejemplo, después de cada 1000 imágenes de entrenamiento. Además, en lugar de usar el conjunto completo de 10 000 imágenes de validación para monitorear el rendimiento, podemos obtener una estimación mucho más rápida usando solo 100 imágenes de validación.

Y así podemos continuar, ajustando individualmente cada hiperparámetro, mejorando gradualmente el rendimiento. Una vez que hemos explorado para encontrar un valor mejorado para $\eta$ , pasamos a encontrar un buen valor para $\lambda$ . Luego experimentamos con una arquitectura más compleja, digamos una red con 10 neuronas ocultas. Luego ajustamos los valores para $\eta$ y $\lambda$ nuevamente. Luego aumentamos a 20 neuronas ocultas. Y luego ajustamos otros hiperparámetros un poco más. Y así sucesivamente, en cada etapa evaluamos el rendimiento utilizando nuestros datos de validación guardados y usamos esas evaluaciones para encontrar hiperparámetros cada vez mejores. A medida que lo hacemos, generalmente lleva más tiempo observar el impacto debido a las modificaciones de los hiperparámetros, por lo que podemos disminuir gradualmente la frecuencia de monitoreo.

Tasa de aprendizaje $\eta$

Observemos que si la tasa de aprendizaje (o learning rate) $\eta$ es muy grande en el descenso del gradiente puede que en lugar de dirigirse al minimo el costo aumente o este oscilando y no llegué al mínimo. Por otra parte si $\eta$ es muy pequeño alcanzar el mínimo llevará demasiado tiempo. Así que podemos realizar lo siguiente: primero, estimamos el valor umbral para $\eta$ en el cual el costo en los datos de entrenamiento comienza a disminuir inmediatamente, en lugar de oscilar o aumentar. Esta estimación no necesita ser demasiado precisa. Puede estimar el orden de magnitud comenzando con $\eta =0.01$ . Si el costo disminuye durante las primeras épocas, entonces debe probar sucesivamente $\eta =0.1,1.0,\dots$ hasta que encuentre un valor para $\eta$ donde el costo oscile o aumente durante las primeras épocas. Alternativamente, si el costo oscila o aumenta durante las primeras épocas cuando $\eta =0.01$ , entonces pruebe $\eta =0.001,0.0001,\dots$ hasta que encuentre un valor para $\eta$ donde el costo disminuya durante las primeras épocas. Seguir este procedimiento nos dará una estimación del orden de magnitud para el valor umbral de $\eta$ . Opcionalmente, puede refinar su estimación para seleccionar el valor más grande de $\eta$ en el que el costo disminuye durante las primeras épocas, digamos $\eta =0,5$ o $\eta =0,2$ (no es necesario que esto sea súper preciso). Esto nos da una estimación para el valor umbral de $\eta$ .

Parada temprana

La detención temprana (o early stopping) significa que al final de cada época debemos calcular la precisión de la clasificación en los datos de validación. Cuando eso deje de mejorar, finalice. Esto hace que establecer el número de épocas sea muy simple. En particular, significa que no necesitamos preocuparnos por averiguar explícitamente cómo el número de épocas depende de los otros hiperparámetros. En cambio, eso se soluciona automáticamente. Además, la detención temprana también nos impide automáticamente el sobreajuste. Esto es, por supuesto, algo bueno, aunque en las primeras etapas de la experimentación puede ser útil desactivar la detención temprana, de modo que pueda ver cualquier signo de sobreajuste y usarlo para informar su enfoque de regularización.

Sugiero utilizar la regla de no mejorar en diez para la experimentación inicial y adoptar gradualmente reglas más indulgentes, a medida que comprenda mejor la forma en que se entrena su red: no mejorar en veinte, no mejorar en cincuenta, y así sucesivamente. Por supuesto, esto introduce un nuevo hiperparámetro para optimizar. Sin embargo, en la práctica, suele ser fácil establecer este hiperparámetro para obtener resultados bastante buenos. De manera similar, para problemas distintos de MNIST, la regla de no mejorar en diez puede ser demasiado agresiva o no lo suficientemente agresiva, según los detalles del problema. Sin embargo, con un poco de experimentación, suele ser fácil encontrar una estrategia bastante buena para detenerse temprano.

Programa de tasa de aprendizaje

Hemos mantenido constante la tasa de aprendizaje $\eta$ . Sin embargo, suele ser ventajoso variar la tasa de aprendizaje. Al principio del proceso de aprendizaje, es probable que los pesos sean muy incorrectos. Por eso, es mejor utilizar una tasa de aprendizaje alta que haga que los pesos cambien rápidamente. Más adelante, podemos reducir la tasa de aprendizaje a medida que realizamos ajustes más precisos en nuestros pesos.

¿Cómo deberíamos establecer nuestro programa de tasa de aprendizaje? Hay muchos enfoques posibles. Un enfoque natural es utilizar la misma idea básica que la de la detención temprana. La idea es mantener la tasa de aprendizaje constante hasta que la precisión de la validación comience a empeorar. Luego, disminuimos la tasa de aprendizaje en cierta cantidad, digamos un factor de dos o diez. Repetimos esto muchas veces, hasta que, digamos, la tasa de aprendizaje sea un factor de 1024 (o 1000) veces menor que el valor inicial. Luego, terminamos.

Tamaño del minilote

Elegir el mejor tamaño de minibatch es un compromiso. Si es demasiado pequeño, no podrá aprovechar al máximo los beneficios de las buenas bibliotecas de matrices optimizadas para hardware rápido. Si es demasiado grande, simplemente no actualizará sus pesos con la suficiente frecuencia. Lo que necesita es elegir un valor de compromiso que maximice la velocidad de aprendizaje. Afortunadamente, la elección del tamaño de minibatch en el que se maximiza la velocidad es relativamente independiente de los otros hiperparámetros (aparte de la arquitectura general), por lo que no necesita haber optimizado esos hiperparámetros para encontrar un buen tamaño de minibatch. Por lo tanto, el camino a seguir es usar algunos valores aceptables (pero no necesariamente óptimos) para los otros hiperparámetros y luego probar varios tamaños de minibatch diferentes, escalando $\eta$ como se indicó anteriormente. Grafique la precisión de la validación en función del tiempo (es decir, tiempo transcurrido real, ¡no época!) y elija el tamaño de minibatch que le brinde la mejora más rápida en el rendimiento. Una vez elegido el tamaño del minibatch, puedes proceder a optimizar los demás hiperparámetros.