Introducción al aprendizaje por refuerzo

Reinforcement Learning (RL) o aprendizaje por refuerzo es un acercamiento computacional al aprendizaje obtenido de la interacción. El cuál esta dirigido a un objetivo. Es aprender qué hacer - como mapear situaciones a acciones - .

El aprendiz debe descubrir que acciones dan la mayor recompensa al ejecutarlas.

- Prueba y error.

- Recompensa retardada.

Son las dos carácteristicas más importantes que distinguen al RL. El tipo de problemas que estudia son aquellos que se formalizan como un Proceso de desición de Markov en el cual se modelizan como un agente es capaz de sentir el estado del ambiente y en cierto grado debe poder tomar acción que afecte ese estado. Y cualquier método bien estudiado que resuelva tales problemas son considerados un método de RL.

Elementos

Política: Define el comportamiento del agente en un paso de tiempo dado. Es un mapeo de los estados percibidos a las acciones a tomar cuando está en esos estados.

Señal de recompensa:Define el objetivo. Esta señal define los eventos buenos y malos para el agente. El objetivo del agente es maximizar la recompensa total que recibe a largo plazo.

Función de valor: Especifica que es bueno en el largo plazo. Mapea cada estado a un valor númerico. El valor de un estado es la cantidad total de recompensa que el agente puede eserar acumular en el futuro, empezando en ese estado.

Modelo: Algo que simula el comportamiento del ambiente o que permite hacer inferencias de como el ambiente se comportará. Los modelos son usados para planear, es decir, decidir un curso de acción considerando las posibles situaciones antes de ser experimentadas.

Observaciones:

En el RL moderno hay métodos en el espectro desde bajo nivel, prueba y error, a alto nivel, planeación deliberada. Es decir, el modelo es opcional.

Mientras que la recompensa determina lo deseable de manera inmediata que son los estados del ambiente, los valores indican lo deseable que son a largo plazo después de tomar en cuenta los estados que son probables de seguir y las recompensas disponibles en esos estados.

Los Markov Decision Process (MDP) son una formalización clásica de una sucesión de toma de decisiones, donde las acciones influencian no solo la recompensa inmediata, sino a las situaciones subsequentes o estados, y a así a las recompenzas futuras.

El aprendiz y el que toma decisiones es llamado el agente.

La cosa con la que se interactua, comprendiendo todo lo que está fuera del agente, es llamado el ambiente.

El ambiente también da la recompensa, valores espaciales númericos que el agente busca maximizar a tráves de la elección de acciones.

El agente y el ambiente interactuán en cada paso de tiempo $t=0,1,\dots$. El agente recibe alguna representación del estado del ambiente, $S_t\in \mathcal{S}$, y en base a eso selecciona una acción $A_t\in \mathcal{A}\mathcal{(}\mathcal{s}\mathcal{)}$.

Un paso de tiempo después, en parte como una consecuencia de su acción, el agente recibe una recompensa que es un número $R_{t+1}\in \mathcal{R}\subset \mathbb{R}$, y se encuentra en un nuevo estado, $S_{t+1}$. El MDP y el agente juntos dan como resultado a una sucesión o trayectoria que empieza: $$S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,\dots$$

En este caso los conjuntos $\mathcal{S},\mathcal{A}$ y $\mathcal{R}$ tiene cardinalidad finita. Y $R_t,S_t$ son variables aleatorias, entonces definimos $$P(s^{\prime },r|s,a)=Pr\{S_t=s^{\prime },R_t=r|S_{t-1}=s,A_{t-1}=a\}$$ para todo $s^{\prime },s\in \mathcal{S},a\in \mathcal{A}(s)$.

Como $P$ es una distribución de probabilidad para cada $s$ y $a$, entonces $$\sum _{s^{\prime }\in \mathcal{S}}\sum _{r\in \mathcal{R}}P(s^{\prime },r|s,a)=1\text{ para todo }s\in \mathcal{S},a\in \mathcal{A}(s).$$

La probabilidad de cada valor posible para $S_t$ y $R_t$ depende únicamente del estado y la acción inmediatamente anteriores, $S_{t-1}$ y $A_{t-1}$ y dados estos, no depende en absoluto de los estados y acciones anteriores. Esto se ve mejor como una restricción no del proceso de decisión, sino del estado. El estado debe incluir información sobre todos los aspectos de la interacción agente-entorno pasada que marcan una diferencia para el futuro. Si es así, se dice que el estado tiene la propiedad de Markov.

A partir de la función dinámica de cuatro argumentos, $P$, se puede calcular cualquier otra cosa que uno quiera saber sobre el entorno, como las probabilidades de transición de estado,recompensas esperadas para pares estado-acción y las recompensas esperadas por el estado-acción-próximo estado.

"Todo lo que entendemos por objetivos y propósitos puede entenderse como la maximización del valor esperado de la suma acumulada de una señal escalar recibida (llamada recompensa)."

Formalicemos la idea de que el objetivo del agente es maximizar la recompensa acumulada en el largo plazo. Dado el paso de tiempo $t$, denotamos por $G_t$ a la devolución, es decir a la suma de recompensas desde el paso $t$ al paso de tiempo final $T$. Es decir, $$G_t=R_{t+1}+R_{t+1}+R_{t+3}+\cdots +R_T,$$ este acercamiento tiene sentido cuando la interacción entre el agente y el ambiente se divide naturalmente en subsecuencias, llamados episodios y cada episodio termina en un estado especial llamado estado terminal. Un episodio sucesivo es independiente del anterior. A este tipo de problemas se le cononcen como tareas episodicas.

Por otra parte exsiten las tareas continuas que siguen continuamente sin limite que no tienen estado terminal, es decir que $T=\mathrm{\infty }$, debido a esto necesitamos otro concepto llamado descuento, el agente intenta seleccionar acciones tales que la sume de recompensas descontadas que recibe en el futuro son maximas. En particular, escoge $A_t$ para maximizar la devolución esperada descontada $$G_t=R_{t+1}+\gamma R_{t+1}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{k=0}^{\mathrm{\infty }}{\gamma }^k{R}_{t+k+1},$$ donde $\gamma$ es un parámetro $0\le \gamma \le 1$, llamado tasa de descuento

Notemos que si $\gamma =0$, el agente solo toma en cuenta la recompensa del siguiente paso, solo la recompensa inmediata. Por otro lado asi como $\gamma$ se acerca a $1$, la devolución toma en cuenta las recompensas más futuras.

Algo importante es que $$\begin{array}{rcl}{G}_t& =& R_{t+1}+\gamma R_{t+1}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+\cdots \\ & =& R_{t+1}+\gamma (R_{t+1}+\gamma R_{t+3}+{\gamma }^2{R}_{t+4}+\cdots )\\ & =& R_{t+1}+\gamma G_{t+1}\end{array}$$ Notemos que esto funciona para todo paso de tiempo $t>T$, incluso si la terminación ocurre en $t+1$, dado que definimos $G_T=0$.

Formalmente la política es un mapeo de los estados a las probabilidades de seleccionar cada posible acción. Si el agente sigue una política $\pi$ en el tiempo $t$, entonces $\pi (a|s)$ es la probabilidad de $A_t=a$ si $S_t=s$.

Los métodos de reinforcement learning especifican como la política del agente cambia dada su experiencia.

La función de valor de un estado $s$ bajo un a política $\pi$ se denota por $v_{\pi }(s)$, es el valor esperado de la devolución empezando en $s$ y siguiendo $\pi$. Para los MDPs, podemos definir $v_{\pi }$ por $$v_{\pi }(s)=\mathbb{E}[G_t|S_t=s]={\mathbb{E}}_{\pi }[\sum _{k=0}^{\mathrm{\infty }}{\gamma }^k{R}_{t+k+1}|S_t=s],\text{ para todo }s\in \mathcal{S},$$ Llamamos a la función $v_{\pi }$ la función estado valor para la política $\pi$.

Similarmente, definimos el valor al tomar una acción $a$ en un estado $s$ bajo la política $\pi$, denotada por $q_{\pi }(s,a)$, como el valor esperado de la devolución empezando por el estado $s$, tomando la acción $a$, y siguiendo la política $\pi$ $$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]={\mathbb{E}}_{\pi }[\sum _{k=0}^{\mathrm{\infty }}{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a].$$ Llamamos $q_{\pi }$ la función acción valor para la política $\pi$.

Una propiedad fuindamental que resulta que tienen las funciones de valor es una relación recursiva, llamada ecuación de Bellman, para cualquier política $\pi$ y cualquier estado $s$, la siguiente considición se sostiene entre el valor de $s$ y el valor de sus posibles estados sucesivos: $$\begin{array}{rcl}{v}_{\pi }(s)& =& {\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & =& {\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_t|S_t=s]\\ & =& \sum _a\pi (a|s)\sum _{s^{\prime }}\sum _{r}p(s^{\prime },r|s,a)[r+\gamma {\mathbb{E}}_{\pi }[G_{t+1}|S_{t+1}=s^{\prime }]]\\ & =& \sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],\text{ para todo }s\in \mathcal{S},\end{array}$$ Expresa una relación entre el valor de un estado y los valores de sus estados sucesores. A partir de cada uno de estos estados, el entorno podría responder con uno de varios estados siguientes, $s_0$, junto con una recompensa, $r$, dependiendo de su dinámica dada por la función $p$. La ecuación de Bellman promedia todas las posibilidades, ponderando cada una por su probabilidad de ocurrencia. Establece que el valor del estado inicial debe ser igual al valor (descontado) del estado siguiente esperado, más la recompensa esperada a lo largo del camino.

Piense en mirar hacia adelante desde un estado a sus posibles estados sucesores, como lo sugiere el diagrama. Cada círculo abierto representa un estado y cada círculo sólido representa un par estado-acción. A partir del estado 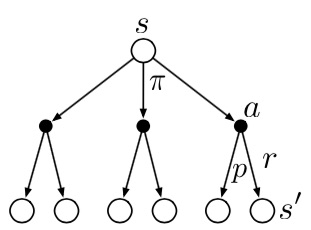$s$, el nodo raíz en la parte superior, el agente podría tomar cualquiera de un conjunto de acciones (se muestran tres en el diagrama) en función de su política $\pi$.

Estas operaciones transfieren información del valor al estado (o par estado-acción) de sus estados sucesores (o par estado-acción).

Resolver una tarea de aprendizaje por refuerzo significa, en líneas generales, encontrar una política que logre una gran recompensa a largo plazo. Para MDP finitos, podemos definir con precisión una política óptima de la siguiente manera. Las funciones de valor definen un ordenamiento parcial de las políticas.

Definición. Una política $\pi$ se dice que es mejor o igual que la política ${\pi }^{\prime }$ si el valor esperado de su devolución es mayor o igual que la de ${\pi }^{\prime }$ para todos los estados. $$\pi \ge {\pi }^{\prime }\text{ si y sólo si }{v}_{\pi }(s)\ge v_{{\pi }^{\prime }}(s)s\in \mathcal{S}.$$

Siempre hay al menos una política que es mejor o igual a todas las demás políticas. Esta es una política óptima. Aunque puede haber más de una, denotamos todas las políticas óptimas por ${\pi }_{\ast }$. Comparten la misma función de valor de estado, llamada función de valor de estado óptima, denotada $v_{\ast }$ y definida como $$v_{\ast }(s)=\underset{\pi }{max}{v}_{\pi }(s)\text{ para todo }s\in \mathcal{S}.$$

Las políticas óptimas también comparten la misma función de valor de acción óptima, denotada $q_{\ast }$, y definida como $$q_{\ast }(s,a)=\underset{\pi }{max}{q}_{\pi }(s,a)\text{ para todo }s\in \mathcal{S}.$$

Como $v_{\ast }$ es la función de valor de una política, debe satisfacer la condición de autoconsistencia dada por la ecuación de Bellman para valores de estado. Sin embargo, como es la función de valor óptima, la condición de consistencia de $v_{\ast }$ se puede escribir en una forma especial sin referencia a ninguna política específica. Esta es la ecuación de Bellman para $v_{\ast }$, o la ecuación de optimalidad de Bellman. Intuitivamente, la ecuación de optimalidad de Bellman expresa el hecho de que el valor de un estado bajo una política óptima debe ser igual al rendimiento esperado para la mejor acción de ese estado: $$\begin{array}{rcl}{v}_{\ast }(s)& =& \underset{a\in \mathcal{A}(s)}{max}{q}_{{\pi }_{\ast }}(s,a)\\ & =& \underset{a}{max}{\mathbb{E}}_{{\pi }_{\ast }}[G_t|S_t=s,A_t=a]\\ & =& \underset{a}{max}{\mathbb{E}}_{{\pi }_{\ast }}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a]\\ & =& \underset{a}{max}{\mathbb{E}}_{{\pi }_{\ast }}[R_{t+1}+\gamma v_{\ast }(S_{t+1})|S_t=s,A_t=a]\\ & =& \underset{a}{max}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\ast }(s^{\prime })].\end{array}$$ Las dos últimas ecuaciones son dos formas de la ecuación de optimalidad de Bellman para $v_{\ast }$. La ecuación de optimalidad de Bellman para $q_{\ast }$ es $$\begin{array}{rcl}{q}_{\ast }(s,a)& =& \mathbb{E}[R_{t+1}+\gamma \underset{a^{\prime }}{max}{q}_{\ast }(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =& \sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{max}{q}_{\ast }(s^{\prime },a^{\prime })].\end{array}$$

Solución análitica a la ecuación

Para MDP finitos, la ecuación de optimalidad de Bellman para $v_{\ast }$ tiene una solución única. La ecuación de optimalidad de Bellman es en realidad un sistema de ecuaciones, una para cada estado, por lo que si hay $n$ estados, entonces hay $n$ ecuaciones en $n$ incógnitas. Si se conoce la dinámica $p$ del entorno, entonces en principio se puede resolver este sistema de ecuaciones para $v_{\ast }$ utilizando cualquiera de una variedad de métodos para resolver sistemas de ecuaciones no lineales. Se puede resolver un conjunto relacionado de ecuaciones para $q_{\ast }$.

Encontrar la política óptima

Una vez que se tiene $v_{\ast }$, es relativamente fácil determinar una política óptima. Para cada estado $s$, habrá una o más acciones en las que se obtenga el máximo en la ecuación de optimalidad de Bellman. Cualquier política que asigne una probabilidad distinta de cero solo a estas acciones es una política óptima. Puede pensar en esto como una búsqueda de un paso. Si tiene la función de valor óptimo, $v_{\ast }$, entonces las acciones que parecen mejores después de una búsqueda de un paso serán acciones óptimas. Otra forma de decir esto es que cualquier política que sea codiciosa con respecto a la función de evaluación óptima $v_{\ast }$ es una política óptima.

Solución aproximada

La solución explícita de la ecuación de optimalidad de Bellman ofrece una vía para encontrar una política óptima y, por tanto, para resolver el problema del aprendizaje por refuerzo. Sin embargo, esta solución rara vez resulta directamente útil. Es similar a una búsqueda exhaustiva, en la que se analizan todas las posibilidades y se calculan sus probabilidades de ocurrencia y sus deseabilidades en términos de recompensas esperadas. Esta solución se basa en al menos tres supuestos que rara vez son ciertos en la práctica:

(1) conocemos con precisión la dinámica del entorno;

(2) tenemos suficientes recursos computacionales para completar el cálculo de la solución;

y (3) la propiedad de Markov.

Para los tipos de tareas que nos interesan, por lo general no es posible implementar esta solución con exactitud porque se violan varias combinaciones de estos supuestos. Por ejemplo, aunque el primer y el tercer supuesto no presentan problemas para el juego de backgammon, el segundo es un impedimento importante. Como el juego tiene alrededor de ${10}^{20}$ estados, se necesitarían miles de años en las computadoras más rápidas de la actualidad para resolver la ecuación de Bellman para $v_{\ast }$, y lo mismo sucede para encontrar $q_{\ast }$. En el aprendizaje por refuerzo, normalmente hay que conformarse con soluciones aproximadas.