Mundo de la cuadrícula

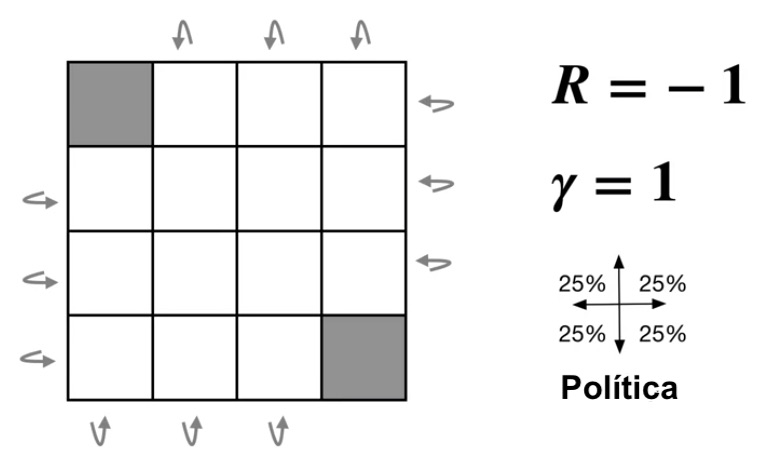
Un ejemplo de un MDP finito episódico sería un agente que está en una cuadrícula rectangular de n×n. Donde las celdas corresponden a los estados del ambiente. En cada estado hay cuatro acciones posibles: arriba, abajo, derecha e izquierda. De manera deterministica causa que el agente se mueva a la celda en la dirección respectiva. Los estados terminales son las celdas grises, (esquina superior izquierda y esquina inferior derecha) y cualquier transcisión tiene una recompensa de −1, por último si la acción lleva a que se salga de la cuadrícula el agente no cambia de celda.

Notemos que la función P(s′,r|s,a) es determinista ya que dado cualquier estado s y la acción a , el estado siguiente s′ al que se llega está completamente determinado y solo hay una posibilidad, además de la recompensa r correspondiente. Así, si estamos en una celda s y tomamos una acción a el agente se moverá a la celda s′, entonces P(s′,r|s,a)=1 y para cualquier otra celda s″≠s′,P(s″,r|s,a)=0.

Recordemos que resolver este MDP significa encontrar una política óptima, para podemos usar directamente el algoritmo de iteración de valor, pero para visualizar los resultados de la mejora, usemos primero evaluación de política y luego mejora de política y finalmente iteración valor.

Evaluación de política

Para ello primero de evaluemos la política que esta dada por la ditribución uniforme que es la que aparece en la imagen, es decir: π(a|s)=14 Aplicaremos el algoritmo de evaluación de política el cual nos permite encontrar una aproximación de la función de valor con una precisición θ. Y necesitamos otro parámetro que es la tasa de descuento, digamos que γ=1 y n=4. Puedes probar con distintos valores de n. En este caso para observar los cambios, haremos una iteración a la vez y omitimos θ.

Inicialicemos la función de valor a 0. Nunca actualizamos el valor del estado terminal, ya que está definido como cero. En la cuadrícula los valores de la función valor para cada estado en la iteración t, presiona el boton para ejecutar una iteración. Observa como se actualizan los valores.

t = 0

Vt:

Vt+1:

0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0

Después de varias iteraciones deja de notarse un cambio en los valores, ya que el cambio es muy pequeño y por simplicidad se redondean a tres decimales.

Mejora de política

Una vez que tenemos la función de valor para una política dada, como se hace la sección previa, podemos obtener una mejor política partir de está función. Actuando codiciosamente sobre dicha función.

Si en la sección anterior hemos iterado lo suficiente, la política generada es la óptima.

Iteración de evaluación y mejora de política

Modifiquemos nuestro MDP para que sea más interesante: en el cual quitamos un estado terminal y agregamos estados malos.

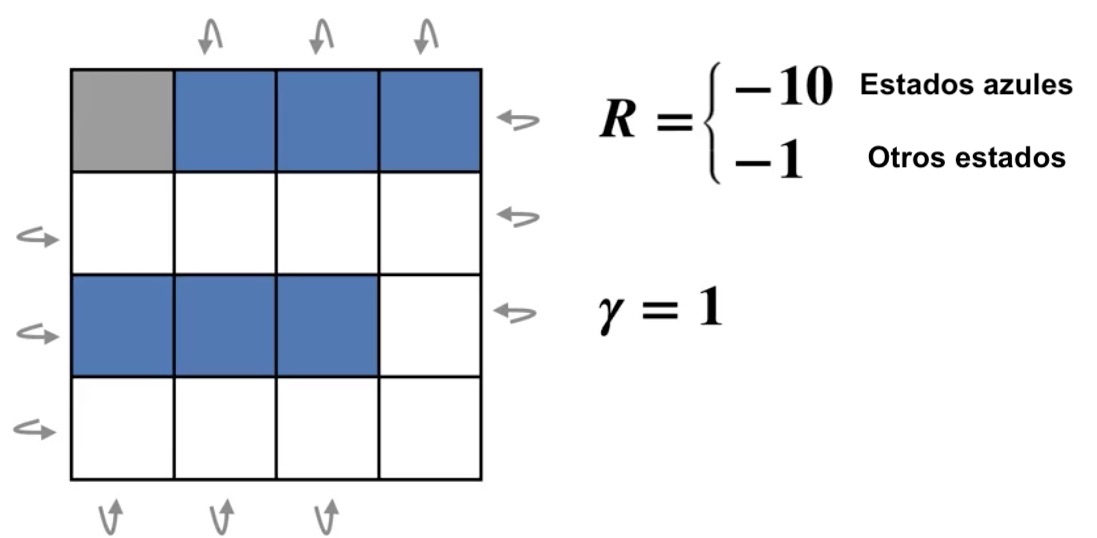
Podemos hacer las dos cosas anteriores de manera que iniciando con una política dada podemos obtener su función de valor, y después generar una política mejor, luego obtener su función de valor correspondiente y volver a empezar hasta que la política enésima ya no cambie.

La función de valor y la política son inicializadas arbitrariamente. En este caso la política de inicializa con la política uniforme para las cuatgro acciones. Y la función de valor en 0 para cada estado.

Iteración de valor

En la sección anterior se puede proceder de dos formas:

1− Podemos iterar en "Evaluar política" hasta la tabla deje de cambiar y entonces "Mejorar política".

2− Podemos alternar en altenar entre "Evaluar política" y "Mejorar política" en cada paso.

La primera opción se puede visualizar de manera intuitiva como:

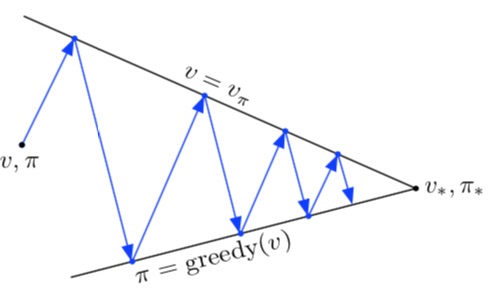
A la segunda opción se le llama iteración de valor. Y se puede ver visualizar en la siguiente figura. 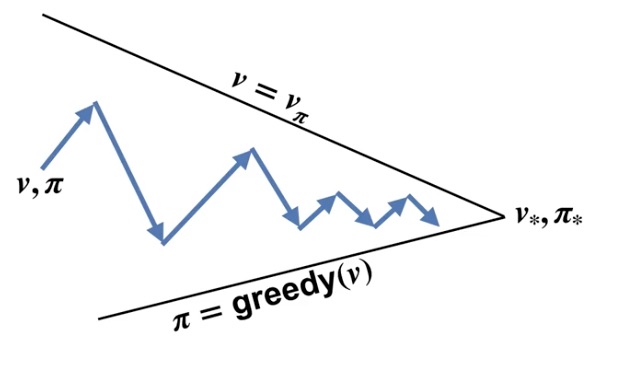Esta opción suele converger más rápido a la política óptima.

Claro que se puede automatizar la realización de las iteraciones añadiendo un parámetro para saber cuando parar y tengamos cierta presición. Podemos parar cuando la diferencia de la función de valor actual con la del paso anterior sea más pequeña que un número positivo pequeño.