Aquí se verá una introducción a un modelo computacional para una computadora cuántica, es decir una descripción matemática sin importarnos la parte del Hardware. Este modelo se llama Quantum circuit model.
¿Qué es un qubit?
Definición.Sean tales que , , entonces un qubit, se define por:
También llamado quantum bit, qbit,Qbit o q-bit. Notemos que y son simplemente vectores, pero es popular usar la notación de Dirac, ya que es práctica para hacer operaciones.
Definición. Sea lineal, definimos la adjunta de por:
Es decir, es la transpuesta conjugada de .
Tenemos que
Consideremos la siguiente notación: y .
Además el producto interno es el siguiente:
Notemos que es una base ortonormal del espacio de Hilbert . A la que llamaremos base computacional.
Así podemos calcular el producto interno de dos estados: y , entonces
En física cuántica las mediciones no son deterministas, sino probabilísticas. En particular, dado cualquier qubit , la probabilidad de obtener 0 es y de obtener 1 es . Naturalmente, estas dos probabildades deben sumar 1, de ahí la necesidad de la condición de normalización. Una vez medido decimos que el qubit ha colapsado al estado. Como obtenemos los resultados que corresponden a y , decimos que son medidos en la base computacional.
Notemos que si es un qubit, y es una base ortonormal de , entonces la probabilidad de medir el resultado asociado a un elemento de una base ortonormal dada es exactamente .
Puertas cuánticas de 1 qbit
Para desarrollar algoritmos útiles, necesitamos una manera de manipular los estados de qubits para hacer cálculos. Para ello usamos las puertas cuánticas así, como en la computanción clásica usamos puertas lógicas para construir circuitos.
Definición. Una matriz unitaria es una matriz tal que .
Proposición.Si es una matiz unitaria, entonces .
Definición. Una puerta cuántica para un solo qubit es una matriz que es unitaria.
Una puerta es la identidad
Una puerta más interesante es la siguiente:
Observemos que pasa con la base
A esta puerta se le llama puerta NOT.
La puerta Hadamard es
a este estado se le llama plus y se denota
a este estado se le llama minus y se denota
Además consideremos estas puertas:
Al conjunto de matrices se le conoce como matrices de Pauli.
Otras dos puertas importantes son:
Observemos que y .
La esfera de Bloch
Como estamos tomando vectores en podríamos pensar que necesitamos una representación en cuatro dimensiones para visualizarlo, pero es posible representar a un qubit en la superficie de una esfera, el cual es un objeto de dos dimensiones.
Sea . Primero vemos que
con y
Entonces existe tal que y , tenemos entonces
Observación.
Sean un número complejo con modulo 1 y un elemento de una base ortonormal. Notemos que
Entonces la no afecta la probabilidad de obtener 0, análogamente con 1. Al hacer la medición respecto a la base computacional. Y por linealidad, al aplicar una puerta cuántica
. Entonces no hay ninguna transformación lineal que nos ayude a distinguir y . Llamamos a una fase global. Mientras que son fases relativas.
Multiplicando a por
donde .
De esta manera podemos describir el estado de cualquier qubit con solo dos números y que podemos interpretar como un ángulo polar y un ángulo azimutal, respectivamente. Es decir, usando coordenadas esféricas tenemos un punto en el espacio tridimensional
que localiza cada estado del qubit en la suerficie de la esfera, llamada esfera de Bloch.

De hecho, esto significa que la compuerta actúa como una rotación de radianes alrededor del eje de la esfera de Bloch... ¡así que ahora sabes por qué usamos ese nombre para la compuerta! De la misma manera, y son rotaciones de radianes alrededor de los ejes y , respectivamente.
Podemos generalizar este comportamiento para obtener rotaciones de cualquier ángulo alrededor de cualquier eje de la esfera de Bloch.
Sea , entonces podemos definir
Notemos que , , , , y .
Propocisión. Para cualquier puerta cuática de un qbit, existe un vector unitario y un angulo tal que
Propocisión. Para cualquier puerta de un qbit, existen angulos tales que
Es algunas arquitecturas es común usar un puerta universal de un qbit que depende de tres angulos y es capaz de generar cualquier otra puerta, su matriz es
Hola, mundo cuántico!
Un circuto se vería asi
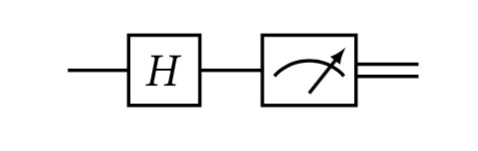 El estado inicial del qubit es , después de aplicar la puerta , entonces el estado cambia a . El simbolo de medidor es justo cuando medidos y el estado del qubit colapsa, en este caso la probabilidad de obtener es y de obtener será . Tenemos un circuito que en teoría genera bits de forma aleatoria siguiendo una distribución uniforme perfectamente.
El estado inicial del qubit es , después de aplicar la puerta , entonces el estado cambia a . El simbolo de medidor es justo cuando medidos y el estado del qubit colapsa, en este caso la probabilidad de obtener es y de obtener será . Tenemos un circuito que en teoría genera bits de forma aleatoria siguiendo una distribución uniforme perfectamente.
Podemos modificar el circuito anterior para obtener cualquier distribución sobre y que queramos. Si queremos que la probabilidad de medir sea , sólo tenemos que considerar y el siguiente circuito:
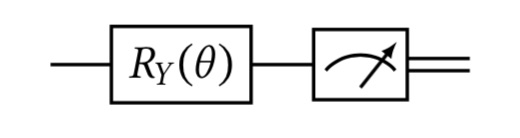
Estados de dos qubits
Por supuesto, en un sistema de dos cúbits, cada uno de los cúbits puede estar en el estado o en el estado . Así, para los dos cúbits, tenemos cuatro combinaciones posibles: ambos están en el estado , el primero está en el estado y el segundo en el estado , el primero está en el estado y el segundo en el estado , o ambos están en el estado . Estas cuatro posibilidades forman una base (llamada base computacional) de un espacio de 4 dimensiones y las denotamos, respectivamente, por
donde es el producto tensorial. El cual se define de esta manera
Por lo tanto, los cuatro estados base se pueden representar mediante vectores de columna de cuatro dimensiones dados por
Generalmente omitimos el símbolo y simplemente usamos alguna de estas notaciones:
o
o incluso
La expresión general para el estado de tal sistema es
donde tales que .
Si medimos en la base computacional que estamos considerando, entonces la probablidad de obtener es .
Supongamos que solo medimos un qubit, digamos que el primer qubit. Entonces la probabilidad de obtener será , que es la suma de las probabilidades de todos los resultados en los que el primer qubit puede ser . Si medimos el primer qubit y el resultado resulta ser , el sistema no colapsará completamente, sino que permanecerá en el estado
La notación de Dirac también es útil para calcular productos internos de estados de dos cúbits. Solo debemos tener en cuenta que
Puertas de dos qubits
Las puertas cuánticas de dos cúbits son matrices unitarias de que actúan sobre vectores columna de dimensiones. La forma más sencilla de construir dichas matrices es tomando el producto tensorial de dos puertas cuánticas de un cúbit. Es decir, si consideramos dos puertas de un qúbit y y dos estados de un qúbit y , podemos formar una puerta de dos cúbits 𝑈1 ⊗ 𝑈2 que actúa sobre como
Por linealidad, podemos extender 𝑈1 ⊗ 𝑈2 a cualquier combinación de estados de dos qúbits y podemos asociar una matriz a 𝑈1 ⊗ 𝑈2. De hecho, dicha matriz viene dada por el producto tensorial de las matrices asociadas a y .
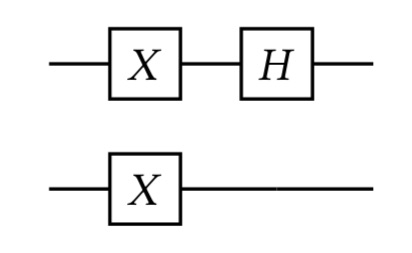
Los productos tensoriales de las puertas se producen de forma natural cuando tenemos circuitos con dos cúbits y pares de puertas individuales de un cúbit actúan sobre cada uno de ellos. Por ejemplo, en el siguiente circuito, la puerta 𝑋 ⊗ 𝑋 actúa sobre los dos cúbits y luego le sigue la puerta 𝐻 ⊗ 𝐼 , donde 𝐼 es la puerta identidad:
La puerta CNOT
Hay muchas matrices unitarias que no se pueden escribir como el producto tensorial de otras matrices simples. En el caso de dos qúbits, probablemente la más importante sea la compuerta NOT controlada (o controlada), normalmente llamada compuerta CNOT, dada por la matriz unitaria
Podemos ver que
Esto significa que el valor del segundo cúbit se invierte si y solo si el valor del primer cúbit es . O, para decirlo en otras palabras, la aplicación de una compuerta NOT en el segundo qúbit (al que llamamos objetivo) está controlada por el primer qúbit. En un circuito cuántico, la compuerta CNOT se representa de la siguiente manera:
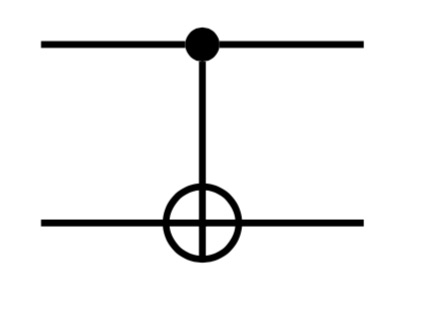 Observe que el qubit de control está indicado por un círculo negro sólido y el qubit de destino está indicado por el símbolo (el símbolo de una puerta también se puede usar en lugar de ).
Observe que el qubit de control está indicado por un círculo negro sólido y el qubit de destino está indicado por el símbolo (el símbolo de una puerta también se puede usar en lugar de ).
Entrelazamiento
Estado producto. Decimos que un estado es un estado producto si se puede escribir como el producto como el producto tensorial de otros dos estados y , cada uno de al menos de un qubit,
Si no es un estado producto, decimos que está entrelazado.
Ejemplo.
Supongamos que
entonces . Si entonces o si entonces . En cualquier caso es imposible llegar a la igualdad. Así se sigue que es estado está entrelazado.
Cuando se miden, los estados entrelazados pueden mostrar correlaciones que van más allá de lo que se puede explicar con física clásica. Por ejemplo si tenemos el estado y medimos el primer qubit puede dar como resultado o , cada uno con una probabilidad de . Sin embargo, si medimos el segundo qubit después, el resultado estará completamente determinado por el valor obtenido al medir el primer qubit y, de hecho, será exactamente el mismo. Si invertimos el orden y medimos primero el segundo qubit, entonces el resultado será o ,
con la misma probabilidad. Pero, en este caso, el resultado de una medición posterior del primer qubit estará completamente determinado.
El teorema de no clonación
Otra propiedad peculiar de los sistemas cuánticos es que, en general, no nos permiten copiar información. Por sorprendente que parezca, es simplemente una consecuencia fácil de la linealidad de las puertas cuánticas. Para demostrar por qué, seamos más precisos sobre lo que necesitaríamos para copiar información, por ejemplo con solo dos qubits. Nos gustaría tener una puerta cuántica de dos qubits que pudiera copiar el primer qubit en el segundo. Es decir, para cualquier estado cuántico dado ), necesitaríamos
Entonces, y y por linealidad
Sin embargo, notemos que el estado original se puede factorizar
Entonces
Llegamos a una contradicción que implica que tal
no existe.
El teorema se aplica a estados desconocidos . Si sabemos qué es —es decir, si conocemos un circuito que prepara a partir de — entonces, por supuesto, podemos crear tantas copias independientes de él como queramos. Sin embargo, si nos entregan sin ninguna información adicional sobre su estado, el teorema de no clonación muestra que no podemos replicar su estado en general.
Puertas controladas
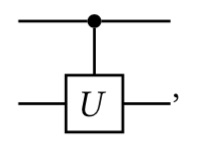
Quizás te preguntes si, además de una puerta controlada-(o CNOT), también existen puertas controladas- , controladas- o controladas-. La respuesta es un rotundo sí y, de hecho, para cualquier puerta cuántica , es posible definir una puerta controlada-(o, simplemente, ) cuya acción sobre la base computacional sea
Se tiene que
La representación del circuito de una puerta C𝑈 es similar a la que usamos para la puerta CNOT, es decir
¡Hola, mundo entrelazado!
Para finalizar nuestro estudio de los sistemas de dos cúbits, vamos a mostrar cómo crear estados entrelazados con la ayuda de la compuerta CNOT. Consideremos el siguiente circuito:
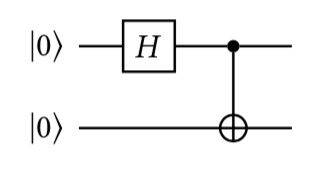
Inicialmente, el estado del sistema es . Después de aplicar la compuerta , llegamos al estado . Finalmente, cuando aplicamos la compuerta CNOT, el estado cambia a , que, como demostramos antes es de hecho un estado entrelazado.
El estado es conocido como un estado de Bell, de los cuales son cuatro. Los otros tres son , , y .
Sistemas multi-qubit
Como ya habrás deducido, si tenemos qubits, los estados que constituyen la base computacional son
Usualmente se omite el simbolo para escribir
o
o simplemente
Por supuesto, un estado genérico del sistema tendrá entonces la forma
sujeto a la única condición de que las amplitudes sean números complejos tales que
.
Obsérvese que la cantidad de parámetros que describen el estado general de un sistema de cúbits cuánticos es exponencial . Para estados altamente entrelazados, no sabemos cómo representar toda esta información de una manera más sucinta y se sospecha firmemente que no es posible. Parte del poder de la computación cuántica proviene de la posibilidad de trabajar implicitamente con números complejos al manipular solo qubits.
Si decidimos medir todos los cúbits del sistema en la base computacional, obtendremos con probabilidad . Si ese es el caso, entonces el estado colapsará a . Pero si solo medimos uno de los cúbits, digamos el -ésimo, entonces obtendremos con probabilidad
donde es el conjunto de números cuyo bit -ésimo es . En este escenario, el estado del sistema después de medir sería
Calcular productos internos de sistemas de -qubits en notación de Dirac es muy similar a hacerlo con sistemas de dos qubits. El procedimiento es análogo al que mostramos al de dos qubits teniendo en cuenta que
Puertas multi-qubit
Dado que los estados de -qubits se representan mediante vectores columna de -dimensiones, las puertas de -qubits se pueden identificar con matrices unitarias de . De manera similar al caso de dos qubits, podemos construir puertas de -qubits tomando el producto tensorial de puertas en un número menor de qubits. Es decir, si es una puerta de -qubits y es una puerta de -qubits, entonces es una puerta de -qubits y su matriz está dada por el producto tensorial de las matrices y .
Sin embargo, hay puertas de -qubits que no se pueden construir como productos tensoriales de puertas más pequeñas. Un ejemplo de ello es la puerta Toffoli o CCNOT, una puerta de tres qubits que actúa sobre la base computacional como
donde es la función XOR y es el símbolo para la función boolena AND. Así, CCNOT aplica una puerta controlada doble en los primeros dos qubits y NOT en el tercer qubit.
A partir de su acción sobre los estados base, deducimos que la matriz para la compuerta CCNOT es:
La puerta de Toffoli es importante porque, utilizándola y con la ayuda de qubits auxiliares, podemos construir cualquier operador booleano clásico. Por ejemplo, (donde es la negación de ) y . Esto demuestra que, con circuitos cuánticos, podemos simular el comportamiento de cualquier circuito digital clásico a costa de utilizar algunos qubits auxiliares adicionales, ya que cualquier función booleana se puede construir solo con negaciones y conjunciones. Esto es algo sorprendente, porque sabemos que todas las puertas cuánticas son invertibles, mientras que no todas las funciones booleanas lo son.
Puertas universales en computación cuántica
Las computadoras cuánticas actuales no pueden implementar todas las puertas cuánticas posibles. En cambio, se basan en resultados de universalidad que muestran cómo cualquier operación unitaria puede descomponerse en un circuito que utiliza un conjunto reducido de puertas primitivas.
Para nosotros será importante saber que, para cualquier operación unitaria, podemos construir un
circuito que la implemente utilizando únicamente puertas de un cúbit y la puerta CNOT. Por esta razón, decimos que esas puertas son universales, en el mismo sentido que, por ejemplo, la negación y la conjunción son universales para la lógica booleana.
Además de las puertas de un cúbit más CNOT, existen muchos otros conjuntos de puertas universales. Por ejemplo, se puede demostrar que las tres puertas , y CNOT se pueden utilizar para aproximar cualquier operación unitaria con cualquier precisión deseada, y son universales en ese sentido.
 El estado inicial del qubit es
El estado inicial del qubit es 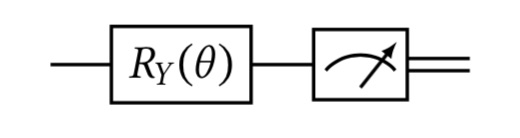

 Observe que el qubit de control está indicado por un círculo negro sólido y el qubit de destino está indicado por el símbolo
Observe que el qubit de control está indicado por un círculo negro sólido y el qubit de destino está indicado por el símbolo 
