Tree LSTM

LSTM estructurados en árbol

Una limitación de las arquitecturas LSTM básica es que solo permiten la propagación de información estrictamente secuencial. Aquí, proponemos dos extensiones naturales de la arquitectura LSTM básica: el árbol de suma de hijos-LSTM y el árbol N-ario-LSTM. Ambas variantes permiten topologías de red más ricas donde cada unidad LSTM puede incorporar información de múltiples unidades hijas.

Al igual que en las unidades LSTM estándar, cada unidad Tree-LSTM (indexada por $j$ contiene puertas de entrada y salida $i_{j}$ y $o_{j}$ , una celda de memoria $c_{j}$ y un estado oculto $h_{j}$ . La diferencia entre la unidad LSTM estándar y las unidades Tree-LSTM es que los vectores de compuertas y las actualizaciones de celdas de memoria dependen de los estados de posiblemente muchas unidades secundarias. Además, en lugar de una única puerta de olvido, la unidad Tree-LSTM contiene una puerta de olvido $f_{j k}$ para cada unidad secundaria $k$ . Esto permite que la unidad Tree-LSTM incorpore selectivamente información de cada unidad secundaria. Por ejemplo, un modelo Tree-LSTM puede aprender a enfatizar las cabezas semánticas en una tarea de relación semántica, o puede aprender a preservar la representación de los hijos ricos en sentimientos para la clasificación de sentimientos.

Al igual que con el LSTM estándar, cada unidad Tree-LSTM toma un vector de entrada $x_{j}$ . En nuestras aplicaciones, cada $x_{j}$ es una representación vectorial de una palabra en una oración. La palabra de entrada en cada nodo depende de la estructura de árbol utilizada para la red. Por ejemplo, en un Tree-LSTM sobre un árbol de dependencia, cada nodo en el árbol toma el vector correspondiente a la palabra principal como entrada, mientras que en un Tree-LSTM sobre un árbol de circunscripción, los nodos de hoja toman los vectores de palabras correspondientes como entrada.

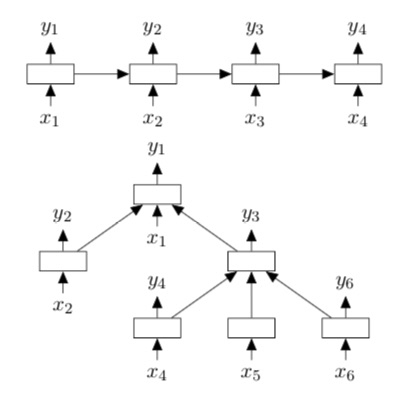
comparacion de la estructura lineal y la de árbol

Árboles de suma de hijos (LSTM)

Dado un árbol, sea $C (j)$ el conjunto de hijos del nodo $j$ . Las ecuaciones de transición del árbol de suma de hijos-LSTM son las siguientes: $\begin{array}{rcl} {\hat{h}}_{j} & = & \sum_{k \in C (j)} h_{k}, \\ i_{j} & = & σ (W^{(i)} x_{j} + U^{(i)} {\hat{h}}_{j} + b^{(i)}), \\ f_{j k} & = & σ (W^{(f)} x_{j} + U^{(f)} h_{k} + b^{(f)}) con k \in C (j) \\ o_{j} & = & σ (W^{(o)} x_{j} + U^{(o)} {\hat{h}}_{j} + b^{(o)}), \\ u_{j} & = & t a n h (W^{(u)} x_{j} + U^{(u)} {\hat{h}}_{j} + b^{(u)}), \\ c_{j} & = & i_{j} ⊙ u_{j} + \sum_{k \in C (j)} f_{j k} ⊙ c_{k}, \\ h_{j} & = & o_{j} ⊙ t a n h (c_{j}), \end{array}$

Intuitivamente, podemos interpretar cada matriz de parámetros en estas ecuaciones como correlaciones de codificación entre los vectores componentes del árbol-LSTM. unidad, la entrada $x_{j}$ y los estados ocultos $h_{k}$ de los hijos de la unidad. Por ejemplo, en una aplicación de árbol de dependencia, el modelo puede aprender parámetros $W^{(i)}$ de modo que los componentes de la compuerta de entrada $i_{j}$ tengan valores cercanos a 1 (es decir, “abierto”) cuando se proporciona como entrada una palabra de contenido semánticamente importante (como un verbo), y valores cercanos a 0 (es decir, “cerrado”) cuando la entrada es una palabra relativamente poco importante (como un determinante).

Árboles de dependencias (LSTM)

Dado que la unidad Child-Sum Tree (LSTM) condiciona sus componentes a la suma de los estados ocultos de los hijos $h_{k}$ , es adecuada para árboles con un alto factor de ramificación o cuyos hijos no están ordenados. Por ejemplo, es una buena opción para árboles de dependencias, donde el número de dependientes de una cabeza puede ser muy variable. Nos referimos a un Child-Sum Tree (LSTM) aplicado a un árbol de dependencias como un Dependency Tree (LSTM).

Árboles N-arios-LSTM

El árbol $N$ -ario-LSTM se puede utilizar en estructuras de árbol donde el factor de ramificación es como máximo $N$ y donde los hijos están ordenados, es decir, se pueden indexar de 1 a $N$ . Para cualquier nodo $j$ , escriba el estado oculto y la celda de memoria de su hijo $k$ como $h_{j k}$ y $c_{j k}$ respectivamente. Las ecuaciones de transición del árbol $N$ -ario-LSTM son las siguientes: $\begin{array}{rcl} i_{j} & = & σ (W^{(i)} x_{j} + \sum_{l = 1}^{N} U_{l}^{(i)} h_{j l} + b^{(i)}), \\ f_{j k} & = & σ (W^{(f)} x_{j} + \sum_{l = 1}^{N} U_{k l}^{(f)} h_{j l} + b^{(f)}), \\ donde k = 1, 2, \dots, N . \\ o_{j} & = & σ (W^{(o)} x_{j} + \sum_{l = 1}^{N} U_{l}^{(o)} h_{j l} + b^{(o)}), \\ u_{j} & = & t a n h (W^{(u)} x_{j} + \sum_{l = 1}^{N} U_{l}^{(u)} h_{j l} + b^{(u)}), \\ c_{j} & = & i_{j} ⊙ u_{j} + \sum_{l = 1}^{N} f_{j l} ⊙ c_{j l}, \\ h_{j} = o_{j} ⊙ t a n h (c_{j}), \end{array}$

La introducción de matrices de parámetros independientes para cada hijo $k$ permite que el modelo $N$ -ary Tree-LSTM aprenda un condicionamiento más detallado sobre los estados de los hijos de una unidad que el Child-Sum Tree-LSTM. Consideremos, por ejemplo, una aplicación de árbol de circunscripciones donde el hijo izquierdo de un nodo corresponde a una frase nominal y el hijo derecho a una frase verbal. Supongamos que en este caso es ventajoso enfatizar la frase verbal en la representación. Entonces, los parámetros $U_{k}^{(f)} l$ pueden entrenarse de manera que los componentes de $f_{j 1}$ estén cerca de 0 (es decir, “olvidar”), mientras que los componentes de $f_{j 2}$ estén cerca de 1 (es decir, “preservar”).

La parametrización de la puerta de olvido.

Definimos una parametrización de la puerta de olvido $f_{j k}$ del késimo hijo que contiene matrices de parámetros “fuera de la diagonal” $U_{k l}^{f}, k \neq l$ . Esta parametrización permite un control más flexible de la propagación de información del hijo al padre. Por ejemplo, esto permite que el estado oculto izquierdo en un árbol binario tenga un efecto excitatorio o inhibidor en la puerta de olvido del hijo derecho. Sin embargo, para valores grandes de $N$ , estos parámetros adicionales son poco prácticos y pueden estar vinculados o fijados a cero.

Árboles de circunscripciones-LSTM

Naturalmente, podemos aplicar unidades de árboles binarios-LSTM a árboles de circunscripciones binarizados, ya que se distinguen los nodos hijos izquierdo y derecho. Nos referimos a esta aplicación de árboles binarios-LSTM como árboles de circunscripciones-LSTM. Nótese que en los árboles de circunscripciones-LSTM, un nodo $j$ recibe un vector de entrada $x_{j}$ solo si es un nodo de hoja.

Referencias

Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks